2. 北京科技大学 北京 100083
2. University of Science and Technology Beijing, Beijing 100083, China
提高效率与促进公平是社会生产与分配所追求的两个核心目标。无论是在“效率优先、兼顾公平”、以经济建设为中心的年代,还是在更加强调公平、建设和谐社会的时期,效率和公平都始终是衡量社会发展的两个重要方面。医药卫生体制改革的目的是提高效率、促进公平,因此,卫生体系效率评价是医药卫生体制改革评价的重要方面。本文构建了卫生体系效率测量的概念框架,并介绍了应用数据包络分析测量卫生体系效率的方法学问题。
卫生体系效率(health system efficiency)是指在卫生资源投入既定的条件下,卫生体系目的的实现程度,定量地表示为实际实现程度与最大可能实现程度之比值。[1]简言之,卫生体系效率是以最少的卫生资源投入实现最优的卫生体系目的。卫生体系效率(或绩效)是卫生政策研究人员一直关心的问题,特别是在卫生体系改革的进程中。2000年前后,世界卫生组织(WHO)全球卫生政策询证项目(Global Program on Evidence for Health Policy)发布了一系列相关研究报告,包括引起广泛争议的2000年世界卫生报告《卫生系统:改进业绩》。[2]在WHO发布的研究报告中,将卫生体系的目的(或目标)界定为三个方面:健康(health)、反应性(responsiveness)和筹资公平(fairness in financing), 作为卫生体系绩效评价的基础框架。[2, 3, 4]但在这个概念框架中,绩效和效率两个术语被赋予了不同的含义,卫生体系的绩效表现为质量、公平和效率三个维度,效率成为绩效测量的一个方面。同时,效率与公平内涵的界定变得模糊不清,效率的测量中包含了公平的内容,即效率要从健康和反应性两个指标的水平与分布,以及筹资公平所构成的三个指标、两个维度去衡量,这给效率测量带来了困难。而事实上,在WHO发布的对卫生体系效率的测量报告中,效率的测量仅包含了健康一个目标。[1, 5]
自2000年的世界卫生报告发布以来的十年间,WHO没有对卫生体系绩效测量报告进行更新。卫生体系的绩效或效率测量,无论是方法学还是实证研究,十年来并没有取得显著的进展。卫生体系效率的测量远比商品生产领域和其它非商品生产领域复杂,但就像Jacobs等所说的那样,我们不能因为困难而放弃[6]。为了使卫生体系效率的测量更具可操作性,逻辑更加清晰,本文重新构建了卫生体系绩效和效率测量的概念框架,并以此为基础介绍了效率测量的指标和模型。
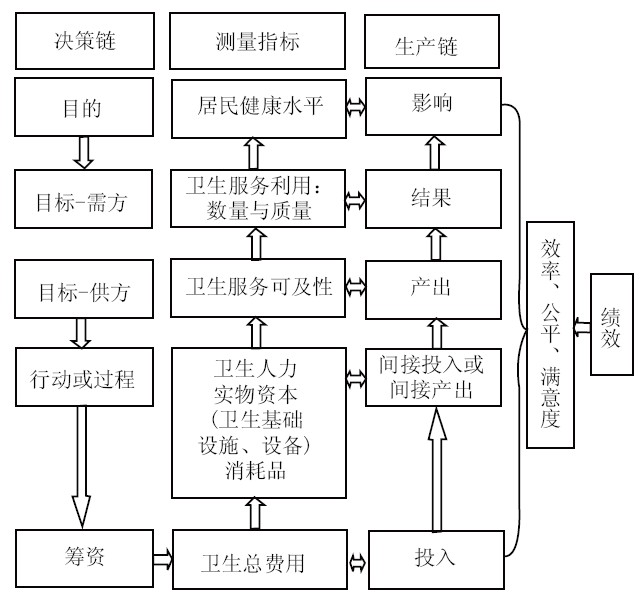
从卫生体系效率的定义出发,卫生体系效率的测量涉及卫生资源的投入和卫生体系目的的实现两个方面。卫生体系目的实现的过程可以认为是一个具有投入和产出的生产过程,但与物质生产领域相比,卫生体系的投入、产出及其生产过程要复杂得多。卫生体系整体可以作为一个宏观的健康生产单位。[4, 7]卫生体系从资源投入到目的实现的决策过程和生产过程可分解为多个阶段(图1)。从决策的逻辑过程看:(1)卫生体系的最终目标是保障和提高居民的健康水平,要达到这一目的,需要保障居民合理的卫生服务利用;(2)卫生服务可及性及其质量是保障居民卫生服务利用的前提条件;(3)卫生人力资源和基础设施、设备与技术是实现卫生服务可及性与质量的基础;(4)卫生筹资是卫生资源的源头。健康生产则是上述决策链的逆过程。效率与公平贯穿于生产过程的各个阶段:公平性不仅表现为筹资的公平性,也表现为卫生资源配置、卫生服务可及性与利用、健康状况等方面的公平性;效率则体现在由前一阶段到后一阶段的生产过程中:由卫生费用到卫生资源,由卫生资源到卫生服务可及性与利用,由卫生服务利用到健康水平的提高。另外,病人(或居民)满意度也是评价卫生服务体系的一个重要方面。
|
图1 卫生体系效率的概念框架 |
由于卫生体系的效率体现在生产过程的各个阶段,其测量途径可以分为两类:黑箱模型和链式模型。黑箱模型是测量从生产过程的入口到出口的效率,将中间过程视为黑箱。投入指标是卫生费用,产出指标则是健康水平,例如期望寿命、5岁以下儿童死亡率、孕产妇死亡率等。链式模型是将生产过程的黑箱打开,把从投入卫生费用到实现健康产出的过程视为一条生产链,可以测量生产链条上各个节点的效率,将前面的节点作为投入,后面的节点作为产出,例如把卫生资源作为投入,把卫生服务利用作为产出。在测量节点的效率时,作为产出的节点往往会受到卫生体系以外因素的影响,越是靠近末端节点,所受到的外部影响越大,例如健康水平会受到教育、宗教、收入等因素的影响。卫生体系的整体效率可由链式模型各节段效率的乘积来表示。
在卫生体系生产链的各个节点,除卫生服务可及性与质量外,均可分别通过一系列的分指标来准确地定量测量(表1)。卫生服务可及性的准确定义和定量测量比较困难。卫生服务可及性可划分为两个维度,即空间(地理)可及性和社会经济可及性。空间(地理)可及性一般通过距离医疗机构的远近或到达医疗机构的时间来测量,社会经济可及性主要是指经济可及性,可通过医疗保险覆盖率、个人支付卫生费用占收入的比例等指标测量。卫生服务可及性还可通过两周患病未就诊率、应住院未住院比例等指标间接地反映。卫生服务质量一般通过间接指标来反映,例如卫生人员学历、诊断符合率、医院感染率、急危重症抢救成功率等。由于卫生服务可及性的测量难度相对较大,从测量的准确性、难易程度和数据可获得性的角度考虑,在实际评价中,卫生体系效率的测量可包括4个节点的指标,即卫生费用、卫生资源、卫生服务利用和健康水平,共组合出6个模型(表2)。
| 表1 卫生体系效率的测量指标 |
| 表2 卫生体系效率的测量方式 |
在进行卫生体系效率的国际间比较时,如果以卫生总费用或其它涉及费用的指标作为投入,需要统一货币单位。换算方法有两种:一是采用实际汇率进行换算,优点是实时更新的各国汇率数据很容易获得;二是采用各国货币的实际购买力,即购买力平价(Purchasing Power Parity, PPP),进行换算。PPP是由世界银行等组织主持的国际比较项目 (International Comparison Program,ICP)计算和发布的国际一致价格跨国比较体系,其计算依据是各国国内商品价格同基准国家(通常以美国美元作为基准)同种商品价格比率的加权平均值。[8]理论上采用PPP进行换算更为合理,但是覆盖世界各国的PPP数据并非每年都有,目前能够获得的数据是世界银行发布的2005年PPP数据。
如果以期望寿命作为产出指标,WHO发布的研究报告建议采用健康调整期望寿命(Health-adjusted life expectancy,HALE)或伤残调整期望寿命(Disability-adjusted life expectancy,DALE)。[5, 9]在WHO发布的部分年份的《世界卫生报告》或《世界卫生统计报告》中,包含了各成员国人口的HALE数据。[10, 11, 12]另外,WHO的报告还建议,不应直接使用HALE作为产出指标,而是需要将卫生体系对HALE的贡献分离出来作为产出指标,即实际的HALE与理论上如果没有任何卫生体系时的HALE之差,这使得分析过程更为复杂。[3, 5]
卫生体系的产出无法直接用货币价值来衡量,因此,卫生体系效率评价一般是采用技术效率的测量方法。
Shephard 1953年提出的效率测量的距离函数和Farrell在1957年提出的技术效率概念为非商品生产领域的效率测量奠定了基础,使在没有价格信息的情况下评价生产效率成为可能。[13]技术效率是指某 个生产单位达到该行业当前技术水平的程度,即在投入既定的情况下,达到产出最大化的程度;用集合的概念表述为从给定投入集合中获得最大产出的能力。技术效率也可从产出的角度衡量,即在产出既定的情况下,达到投入最小化的程度。限于篇幅,关于技术效率和距离函数的详细介绍参见Coelli 等的著作。[14]
技术效率测量的基础是距离函数,根据距离函数计算方法的不同,可以将技术效率测量方法分为多种类型。按照是否需要设定生产函数可划分为参数方法和非参数方法;按照是否考虑随机误差可划分为固定前沿方法和随机前沿方法。截面数据和面板数据的效率分析方法中最常用的是数据包络分析(Data envelopment analysis, DEA)和随机前沿分析(Stochastic frontier analysis, SFA)。数据包络分析属于固定前沿非参数方法,随机前沿分析属于参数方法。数据包络分析的主要优点是计算简单,不需设定生产函数,处理多投入、多产出的问题和处理单投入、单产出的情况一样方便;缺点是数据处理没有考虑随机误差,不能直接对结果做出统计推断。随机前沿分析的主要优点是考虑了随机误差,容易对分析结果做出统计推断;缺点是计算复杂,对样本量要求较高,并且对无效率项的统计特征有严格的要求,不容易处理多产出的问题,如果生产函数设置不当会严重影响结果的准确性。数据包络分析与随机前沿分析方法的详细比较参见Jacobs等[6]和Hollingsworth 等的著作。[15]数据包络分析和随机前沿方法在卫生体系效率分析中的应用情况参见文献。[15, 16, 17, 18, 19]
面板数据固定效应非时变模型是WHO在2000年测量191个会员国的卫生体系效率时所采用的方法。[1, 5]该方法的主要优点是计算简单,缺点是其假定在测量的时间跨度内各单位的效率是恒定不变的,这样的假设显然与实际情况不符,由于许多国家处于卫生体系和卫生政策的变革过程中,而卫生改革可能会促进或降低卫生体系的效率。在面板数据随机前沿分析方法中(固定效应或随机效率模型),可以加入时变的因素,但其假定所有测量单位的时变效应相同。[20]这点与实际情况也不符合,因为有的国家的改革可能促进卫生体系效率的提升,而有的国家的改革可能会降低卫生体系的效率。在处理时变的问题上,数据包络分析方法具有更强的灵活性,DEA-Malmquist模型可以方便地分别计算每个单位生产率的动态变化情况,并且可以将生产率的变化进一步分解为相对效率变化和效率前沿移动。[21]
DEA是一种基于被评价对象间相对比较的非参数技术效率分析方法,这一分析方法是由美国的Charnes,Cooper和Rhodes等三人于1978年首次提出的,因此后来将DEA的第一个模型命名为CCR模型。[22]DEA对于分析多投入、多产出的情况具有特殊的优势,因而其应用范围不断扩展,DEA已经成为融汇了运筹学、管理学、计量经济学、数学和计算机科学等多学科的重要研究领域。[23, 24]DEA在卫生领域也得到了广泛应用。[6, 15, 16, 17, 18, 19]
按照对效率的测量方式,DEA模型可分为投入导向(input-oriented)、产出导向(output-oriented)和混合导向(也称为无向,non-oriented)。投入导向模型是从投入的角度对被评价DMU无效率程度进行测量,测量的是要达到技术有效各项投入应该减少的程度;产出导向模型是从产出的角度对被评价DMU无效率的程度进行测量,测量的是要达到技术有效各项产出应该增加的程度;混合导向模型则是同时从投入和产出两个方面进行测量。模型导向的选择主要取决于分析目的。如果分析目的只是获得各单位的效率值,上述三种导向的模型均可。如果需要做进一步的投影分析,从管理角度考虑,如果把减少投入作为对无效率单位提高效率的主要途径,应选择投入导向模型;如果把增加产出作为提高效率的主要途径,则应选择产出导向模型。需要特别注意的是,如果在卫生资源投入不足的背景下,选择投入导向模型会使得投影分析的结果不容易进行解释。因为在投入导向模型中,根据投影分析的结果,无效率的单位要达到有效率的状态,其改进目标是减少投入,这似乎与卫生资源投入不足的背景产生矛盾(但实质上并不矛盾),使得分析结果容易产生误解。另外,在分析卫生服务效率时,在需求不足的背景下(当需求是决定卫生服务产出数量的首要因素时),选择产出导向模型,会使得投影分析所确定的产出目标客观上难以实现,从而失去实际指导意义。
在DEA模型中,根据生产技术规模报酬的类型,可分为规模报酬不变(constant returns to scale, CRS)、可变(variable returns to scale, VRS)、非增(non-increasing returns to scale, NIRS)和非减(non-decreasing returns to scale, NDRS)4类模型。[25]根据健康生产理论,卫生体系的生产技术是规模报酬可变的,因此在评价卫生体系的技术效率时,应选择VRS模型。[26, 27]另外,选择CRS模型会产生不合理的投影分析结果。例如在分析各个国家 卫生体系的效率时,如果以期望寿命作为产出指标,在产出导向模型的投影分析结果中,投入较大而效率较低的国家的目标值可能会超出合理的范围(比如目标值为200岁)。
VRS模型(以产出导向为例)的数学表达式为:

其中,X表示投入矩阵,Y表示产出矩阵,x0和y0表示被评价单位的投入和产出向量;约束条件∑ j λj=1使参比限制在相似生产规模的水平上。效率值θ=1/φ。
与随机前沿分析方法相比,DEA所需要的最小样本数量相对较小。但是如果样本数量过少,指标数量过多,就会造成分析结果不稳定,并且容易出现由于缺少参照而默认有效的问题(efficient by default)。一般认为,样本数量不应少于投入和产出指标数量的3倍,并且不少于投入和产出指标数量的乘积。[28, 29, 30]所需样本量的大小不仅取决于投入、产出指标的数量,还受到数据分布的影响,上述对样本量的要求可以看作是最低要求:如果不满足上述条件,DEA分析结果的区分度通常会很低;但是满足上述条件,也不一定能够获得满意的区分度。由于不同的分析目的对效率区分度的要求不同,样本数量是否足够的最终判断标准是DEA模型的效率区分度是否能够满足分析的需要。在样本数量一定的条件下,只能通过减少投入或产出指标数量的方式来提高效率分析结果的区分度。
在VRS模型中,有两个造成默认有效的充分(但非必要)条件(只需满足下面的条件之一即可):(1)有一个或多个投入指标的数值最小;(2)有一个或多个产出指标的数值最大。在这样的条件下,被评价决策单元没有相似规模的其它决策单元进行参比,从而形成默认有效的结果。默认有效的决策单元可能处于两种状态:一是确实处于生产前沿;二是仅仅是因为缺少参照而被判定为有效。
判断VRS模型默认有效的充分和必要条件是投入导向或产出导向“超效率”(Super-efficiency)模型无可行解。默认有效的DMU要么会在产出导向的超效率模型中,因无法构建与自身投入规模相同的标杆而导致无可行解;要么会在投入导向的超效率模型中,因无法构建与自身产出规模相同的标杆而导致无可行解。[31, 32, 33]所以超效率模型是判断有效的决策单元是否为默认有效的一种方法。
VRS超效率模型(以产出导向为例)的数学表达式为:
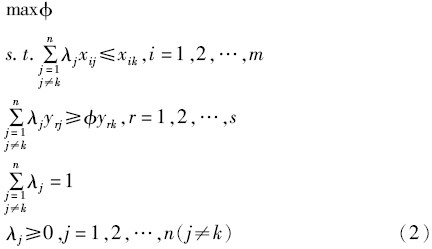
在超效率模型中,被评价决策单元参照的生产前沿是由其它决策单元构成的,不包括其自身,使效率值可能会超过1,从而可以对有效的决策单元进行进一步区分。
默认有效并非意味着其作为参比标杆的意义不重要。被评价为有效的决策单元(包括默认有效的决策单元)作为标杆的重要性可通过被其它决策单元参比的次数来判断,被参比的次数越多,标杆意义越大;在VRS模型中还可以参考每个有效的决策单元构建标杆的权重系数(lambda)的总和,总权重越大,标杆意义越大。
在卫生体系的生产过程中存在着影响健康或卫生服务提供,但却是卫生体系所无法控制的因素,例如人口的受教育程度、收入水平、人口密度,甚至气候、环境等。针对这类问题有两种处理方法:一是采用包含不可控因素的DEA模型;二是在DEA分析之后进行进一步的回归分析,确定这些影响因素对效率的影响。
包含不可控因素的DEA模型一般是将这类不可控因素转换为投入指标处理,例如人群的教育水平越高,健康状况越好,因此将教育水平作为健康产出的投入之一,但是在模型中对不可控投入和可控投入进行不同的处理。[34]以投入导向VRS模型为例,其线性规划方程为:

在约束条件中不可控投入与效率值θ不发生直接关系,并且在确定被评价DMU投入的目标值时仅使用可控投入,这使得不可控投入的作用仅限于保证参比的合理性,其原理类似于统计分析中对混杂因素的处理。在文献中,不同的学者对这一类DEA模型有不同的命名。最先提出这一模型的Banker 和Morey将其称为具有外生不可控投入和产出的DEA模型(exogenously fixed inputs and outputs beyond the discretionary control of DMU managers)[34],Zhu将这一模型称为measure specific model[35],Cooper称之为不可控变量模型(nondiscretionary variable model)[25]。
在采用回归模型分析影响因素时,如果因变量是DMU的效率状态,即有效和非有效,可以采用logistic回归模型;如果因变量是效率值,当有效DMU(效率值为1)的数量较少时,可采用一般线性回归模型;当样本中有效DMU较多时,应采用能够处理截尾值的Tobit回归模型。因为标准的DEA模型无法对有效的DMU进行进一步的区分,效率值1可以看作是截尾数据(单侧截尾)。此外,为了避免出现效率值的截尾问题,可以采用超效率(super-efficiency) DEA模型。[31]
需要注意的一点是,无论是对效率的影响因素进行回归分析,还是更为常见的对效率值进行排序,其潜在的假设是DEA模型得出的各DMU的效率值是可比的。DEA模型得出的效率值的可比性因具体模型和分析目的而异:
(1)DEA效率值θ表示被评价DMU达到当前技术水平(即生产前沿的技术效率)的程度;1-θ表示与生产前沿相比,被评价DMU无效率的程度,也可理解为无效率DMU提高效率的潜力。如果测量目的是比较各DMU达到生产前沿技术效率水平的程度,则DEA效率值是可比的。
(2)在评价各DMU的效率时,不同的DMU在生产前沿上的参照点是不同的。生产前沿上的不同参照点对于达到生产目的的意义或重要性可能存在差异(例如单次住院服务和单次门诊服务对于提高居民的健康水平的贡献不同)。如果测量目的是比较各DMU实现最终生产目的的效率,即以最少的投入实现最好的生产目的,此时DEA效率值是否具有可比性取决于各测量指标对于生产目的是否具有同等的意义。
反映卫生体系投入和产出的指标有很多是率或比值(以下简称“率”)的形式,例如卫生总费用占GDP的比例、服务覆盖率、死亡率、发病率、患病率等。DEA模型是基于生产可能集理论的线性规划方法,如果直接采用率作为投入或产出指标,在CRS模型中,投影分析的结果中会出现率的目标值大于1的情况。虽然采用VRS模型可以避免出现率的目标值大于1的问题[36],但是VRS模型仍然存在DEA模型确定的生产前沿处于生产可能集之外的问题[30]。当投入或产出指标中存在率时,可以采用两种方法对这些指标进行特殊处理。[30]
以产出导向的VRS模型为例,第一种方法是将率的分子作为产出指标,而将率的分母作为投入指标,其线性规划方程表示为:

其中,N和D分别表示率指标的分子和分母,n0和d0分别表示被评价DMU该率指标的分子和分母。
第二种方法是在线性规划方程的左边将率指标拆分为分子指标和分母指标,分别进行线性运算,但是在方程的右边不对被评价DMU的率指标进行拆分,其线性规划方程表示为:

其中,N和D分别表示率指标的分子和分母,r0表示被评价DMU的率指标。
第一种方法的优点是保持了模型的线性规划,缺点是增加了投入或产出指标的数量,从而增加了对样本量的要求;第二种方法的优点是没有增加投入和产出指标数量,但模型变为非线性规划问题。另外,两种方法均要求必须获得率指标的分子和分母数据。
卫生体系数据不仅存在大量率指标,而且在这些率中,有很多是负向指标,即率越低越好,例如死亡率、发病率、患病率等。在DEA文献中有许多处理负向指标(在文献中通常称为undesirable outputs,非期望产出,或bad outputs,坏产出)的方法,例如将负向产出指标作为投入指标[35];将负向指标作为负值指标,然后通过坐标变换使得负值指标变为正值,但坐标变换后只能保持效率状态(有效或非有效)不变,而效率值会发生改变[37, 38, 39]。
传统的DEA模型不能处理包含负数的指标,但是对传统的DEA模型进行一些改进之后,可以使其具备处理负数指标的能力, 以投入导向VRS模型为例, 方法如下[40]:
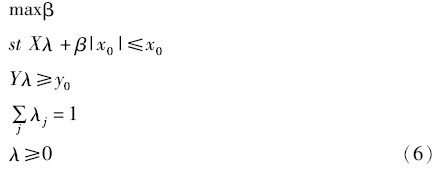
其中,|x0|表示x0的绝对值,β表示被评价DMU无效率的程度,效率值表示为θ=1-β。改造后的DEA模型(6)与文献中最常用的处理负向产出指标的方向距离函数模型的结果是一致的。[41]
由于卫生数据中的许多指标具有“率”和“负向”的双重特征,为解决这一问题,在文献中往往是将负向指标转换为正向指标,例如将死亡率转换为生存率(生存率=1-死亡率)。[42, 43, 44]这种转换方法在VRS模型中只能保证效率状态(是否有效)保持不变,但效率值会发生改变[37, 45, 46]。如果将这种转换方法应用于数值很小的率指标(例如孕产妇死亡率),分析结果会造成很大的差异。举个简单的例子,采用孕产妇死亡率作为产出指标评价卫生体系效率。2010年中国监测地区孕产妇死亡率为30/10万,假设与通过国际间比较确定的生产前沿相比,中国的目标值为25/10万,则中国的效率值为25/30=0.8333;如果采用生存率作为产出指标,则2010年中国监测地区“孕产妇生存率”为99970/10万,目标值为99975/10万,效率值为99970/99975=0.9999。
如果将上文中处理率指标的方法与处理负数指标的方法结合起来使用,则可以解决“负向率指标”的问题。以包含负向率指标的产出导向VRS模型为例:
第一种方法是首先将负向率指标表示为负数率指标,然后再分解为负数分子和正数分母两个产出指标。需要注意的是,与正向率指标的处理方式不同,在此分子和分母都作为产出指标,其线性规划式表示为:

N和D分别表示率指标的分子和分母,其中N为负数指标,由于率的分母属于不可控因素,所以在模型中作为不可控产出指标处理;n0和d0分别表示被评价DMU该率指标的分子和分母,其中n0为负数指标。
第二种方法是也是将负向率指标表示为负数率指标,然后再分解为负数分子和正数分母两个产出指标,但分解后的指标只用于规划方程的左边,其线性规划式表示为:
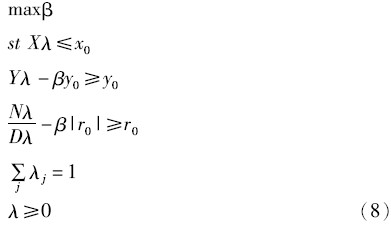
式(7)和式(8)中的β与式(4)和式(5)中的φ的关系为φ=1+β。在产出导向模型中,效率值θ一般表示为θ=1/φ=1/(1+β)。
效率评价是卫生体系研究的重要内容,本文提出的概念框架使卫生体系效率评价的可操作性更强。数据包络分析在卫生领域的应用越来越多,但与其它领域相比,卫生体系效率测量具有许多的特殊性,在应用数据包络分析时,需要特别注意方法学问题。
| [1] | Evans D B, Tandon A, Murray C J, et al. Comparative efficiency of national health systems: cross national econometric analysis [J]. BMJ, 2001, 323(7308): 307-310. |
| [2] | World Health Organization. World Health Report 2000 [R]. Geneva, 2000. |
| [3] | Murray C J, Frenk J. A WHO framework for health system performance assessment [R]. World Health Organization, 2000. |
| [4] | Tandon A, Murray C J, Lauer J A, et al. Measuring overall health system performance for 191 countries [R]. World Health Organization, 2000. |
| [5] | Evans D B, Tandon A, Murray C J, et al. The comparative efficiency of national health systems in producing health: An analysis of 191 countries [R]. World Health Organization, 2000. |
| [6] | Jacobs R, Smith P C, Street A. Measuring efficiency in health care: analytic techniques and health policy [M]. Cambridge University Press, 2006. |
| [7] | Auster R, Leveson I, Sarachek D. The Production of Health, an Exploratory Study [J]. The Journal of Human Resources, 1969, 4(4): 411-436. |
| [8] | 2005 International Comparison Program, Global Purchasing Power Parities and Real Expenditures [R]. The International Bank for Reconstruction and Development/The World Bank, 2008. |
| [9] | Murray C J L, Evans D B. Health systems performance assessment: debates, methods and empiricism [M]. World Health Organization, 2003. |
| [10] | World Health Organization. World Health Report 2002 [R]. Geneva, 2002. |
| [11] | World Health Organization. World Health Report 2004 [R]. Geneva, 2004. |
| [12] | World Health Organization. World Health Statistics 2010 [R]. Geneva, 2010. |
| [13] | Shephard R W. Cost and production functions [M]. Princeton: Princeton University Press, 1953. |
| [14] | Coelli T J, Prasada Rao D S, O’Donnell C J, et al. Introduction to Efficiency and Productivity Analysis [M]. 2nd ed. New York: Springer Science + Business Media, 2005. |
| [15] | Hollingsworth B, Peacock S. Efficiency measurement in health and health care [M]. Routledge, 2008. |
| [16] | Hollingsworth B. Non-parametric and parametric applications measuring efficiency in health care [J]. Health Care Management Science, 2003, 6(4): 203-218. |
| [17] | Worthington A C. Frontier efficiency measurement in health care: A review of empirical techniques and selected applications [J]. Medical Care Research and Review, 2004, 61(2): 135-170. |
| [18] | Hollingsworth B. The Measurement of Efficiency and Productivity of Health Care Delivery [J]. Health Economics, 2008, 17(10): 1107-1128. |
| [19] | Hussey P S, de Vries H, Romley J, et al. A Systematic Review of Health Care Efficiency Measures [J]. Health Services Research, 2009, 44(3): 784-805. |
| [20] | Stevens P, Economic N I O, Research S. Stochastic frontier analysis [M]. NIESR, 2004. |
| [21] | Färe R, Grosskopf S, Lindgren B, et al. Productivity changes in Swedish pharamacies 1980-1989: A non-parametric Malmquist approach [J]. Journal of Productivity Analysis, 1992, 3(1-2): 85-101. |
| [22] | Charnes A, Cooper W W, Rhodes E. Measuring the efficiency of decision making units [J]. European Journal of Operational Research, 1978, 2(6): 429-444. |
| [23] | Seiford L M. Data envelopment analysis: The evolution of the state of the art (1978-1995) [J]. The Journal of Productivity Analysis, 1996, 6(7): 99-137. |
| [24] | Cook W D, Seiford L M. Data envelopment analysis (DEA)-Thirty years on [J]. European Journal of Operational Research, 2009, 192(1): 1-17. |
| [25] | Cooper W W, Seiford L M, Tone K. Data envelopment analysis: a comprehensive text with models, applications, references and DEA-Solver software [M]. 2nd ed. New York: Springer Science + Business Media, 2007. |
| [26] | Gravelle H, Wildman J, Sutton M. Income, income inequality and health: What can we earn from aggregate data? [J]. Social Science & Medicine, 2001(54): 577-589. |
| [27] | Hollingsworth B, Wildman J. The efficiency of health production: re-estimating the WHO panel data using parametric and non-parametric approaches to provide additional information [J]. Health Economics, 2003, 12(6): 493-504. |
| [28] | Ruggiero J. Impact assessment of input omission on DEA [J]. International Journal of Information Technology and Decision, 2005, 4(3): 359-368. |
| [29] | Cooper W W, Seiford L M, Tone K. Introduction to data envelopment analysis and its uses: with DEA-solver software and references [M]. Springer, 2006. |
| [30] | Emrouznejad A, Amin G R. DEA models for ratio data: Convexity consideration [J]. Applied Mathematical Modelling, 2009, 33(1): 486-498. |
| [31] | Andersen P, Petersen N C. A procedure for ranking efficient units in data envelopment analysis [J]. Management Science, 1993, 39(10): 1261-1265. |
| [32] | Zhu J. Robustness of the efficient DMUs in data envelopment analysis [J]. European Journal of Operational Research, 1996, 90(3): 451-460. |
| [33] | Seiford L M, Zhu J. Infeasibility of super-efficiency data envelopment analysis models [J]. Infor, 1999, 37(2): 174-187. |
| [34] | Banker R D, Morey R C. Efficiency analysis for exogenously fixed inputs and outputs [J]. Operations Research, 1986, 34(4): 513-521. |
| [35] | Zhu J. Quantitative Models for Performance Evaluation and Benchmarking: DEA with Spreadsheets [M]. 2nd ed. Boston: Springer, 2009. |
| [36] | Hollingsworth B, Smith P. Use of ratios in data envelopment analysis [J]. Applied Economics Letters, 2003, 10(11): 733-735. |
| [37] | Seiford L M, Zhu J. Modeling undesirable factors in efficiency evaluation [J]. European Journal of Operational Research, 2002, 142(1): 16-20. |
| [38] | Fare R, Grosskopf S. Modeling undesirable factors in efficiency evaluation: Comment [J]. European Journal of Operational Research, 2004, 157(1): 242-245. |
| [39] | Seiford L M, Zhu J. A response to comments on modeling undesirable factors in efficiency evaluation [J]. European Journal of Operational Research, 2005, 161(2): 579-581. |
| [40] | Cheng G, Zervopoulos P, Qian Z, A variant of radial measure capable of dealing with negative inputs and outputs in data envelopment analysis (Working Paper) [R]. China Center for Health Development Studies, Peking University, 2011. |
| [41] | Chung Y H, Färe R, Grosskopf S. Productivity and undesirable outputs: A directional distance function approach [J]. Journal of Environmental Management, 1997, 51(3): 229-240. |
| [42] | Alexander C A, Busch G, Stringer K. Implementing and interpreting a data envelopment analysis model to assess the efficiency of health systems in developing countries [J]. IMA Journal of Management Mathematics, 2003, 14(1): 49-63. |
| [43] | Afonso A, St Aubyn M. Non-parametric approaches to education and health efficiency in OECD countries [J]. Journal of Applied Economics, 2005, 8(2): 227-246. |
| [44] | Grosskopf S, Self S, Zaim O. Estimating the efficiency of the system of healthcare financing in achieving better health [J]. Applied Economics, 2006, 38(13): 1477-1488. |
| [45] | Lovell C A K, Pastor J T. Units invariant and translation invariant DEA models [J]. Operations Research Letters, 1995, 18(3): 147-151. |
| [46] | Pastor J T. Translation invariance in data envelopment analysis: A generalization [J]. Annals of Operations Research, 1996, 66: 93-102. |
(编辑 薛 云)




