假设1： 在一定时间T范围内，当t∈(0,T)，医院的门诊、急诊病人的流量N(t)服 从强度(参数)为λ的泊松过程，即有

假设2： 在一定时间T范围内，医院住院病人的数量是由门、急诊病人数量决定的。假 定门诊或急诊病人以q(0q1)概率转为住院病人，这种转移可能是立即转移也可能有一 定的延迟，长时间来看这种顺延转移有一定稳定性，所以统一假定门诊或急诊病人，统一以q(0q1) 概率立即转为住院病人。显然，当t∈(0,T)，若住院病人的流量为X(t)，则根据假设1知X(t)=0,1,2,…。

假设3： 不存在诱导需求，即表明病人住院可能性的概率为q是客观的，不存在人为因 素诱导病人去住院。本假设是为了简化模型，所作的非必要的假设。

假设4： 在一定时间T范围内，当t∈(0,T)，病人的住院天数Y_i(i=1,2,…,X(t))相互独 立同分布，且Y的期望值EY存在。

假设5： 病床的使用率为100%，几乎不存在病床的空置。本假设也是为了简化模型， 所作的非必要的假设。当然，由于中国一些大型综合医院人满为患，住院出现了排 队现象，事实上病床使用率接近甚至超过了100%。

根据以上假设得出以下命题结论：

命题1： 在一定时间T范围内，当t∈(0,T)，住院病人的流量X(t)服从强度为λq的泊松 过程。

证明：

因为病人住院可能性的概率为q，那么其不住院的概率就为1-q。很容易知道，在病人的数量N(t)的条件下住院病人数X(t)的分布律为：

由(1)式可以看出，在病人数量N(t)的条件下住院病人数X(t)的分布律，显然是一个二项分布。所以，结合(1)式并根据全概率公式得出： P｛X(t)=k｝ =∑^∞_n=kP｛N(t)=n｝P｛X(t)=k｜N(t)=n｝

这就证明了命题1。

命题2： 在一定时间T范围内，当t∈(0,T)，病人i的住院天数Y_i(i=1,2,…,X(t))，若记 作Z(t)=∑^X(t)_i=1Y_i为复合泊松过程^{[8, 9]}，则有,E[Z(t)]=λqtE(Y)。

证明：

利用特征函数来证明，记Y_i的特征函数φ_Yi(u)=E(e^jY_iu)，(其中， j²=-1)。那么，病人住院天数 样本总体Y的特征函数φ_Y(u)=φ_Yi(u)=E(e^jY_iu)。

根据特征函数的性质，显然有φ_Y(0)=1 (3)

(-j)^kφ^(k)_Y(0)=E(Y^k),k=1,2,… (4)

其中，E(Y^k)表示Y的k阶矩，或Y^k的期望值。

故结合(3)式与(4)式，可以计算Z(t)的特征函数φ_Z(t)，且有：

所以参照(3)、(4)和(5)式，再根据特征函数的性质很容易得出：

因此，命题2得证。

为研究的需要，要确定一天需要多少床位来满足住院病人的需求，设定t=1，即只 考虑一天之内的门诊病人流量。因此，根据以上假设及命题1、命题2，很容易得出命题3、 命题4以及命题5：

命题3： 在一天时间内，医院的病人数N(1)服从参数为λ的泊松分布，即

命题4： 在一天时间内，住院病人的流量X(1)服从参数为λq的泊松分布，即

命题5： 在一天时间内，住院病人i的住院天数Y_i(i=1,2,…,X(t))，若记作Z(1)=∑^X(t)_i=1Y_i为复合泊松过程，则有E[X(1)]=λqE(Y)。

如果住院病人的需求较多而医院的床位供不应求，住院病人则会转到其它医院，这会给医 院带来损失，所以西方国家在20世纪后半叶，就出现许多医院床位空置的现象，这是为了 防止过多需求可能带来的损失，这就意味着如果需求超出了服务能力，那么超额需求就得不 到服务，所以一些特定的行业总是要保持充分大的服务能力，以保证高于随机需求。^[10]另 外，如果住院病人相对较少，而医院提供了过多的床位数量，将会增加医院 的不合理运营成本，也会给医院带来损失。20世纪后期，西方一些文章对医院床位空置产生的成本进行 了测算。^{[10, 11, 12, 13]}

因此，需要引入一个衡量机会成本与空置成本的损失函数L估算最优床位规模Z^*。假 设医院有关床位使用涉及了这两类成本：(a)床位相对不足的机会成本；(b)床位相对过 多产生的空置成本。

一天内需要的床位数Z(1)是个随机变量，假设Z^*为最优床位数。因此L的大小由绝 对值｜Z^*-Z(1)｜的大小决定，通过简化的处理，设定损失函数L=A[Z^*-Z(1)]²,(A＞0)。

所以损失函数的期望为，

根据(7)式，为了使得E(L)最小，由E(L)的一阶条件，则有Z^*＝E[Z(1)]。根据命题5知，Z^*=E[Z(1)]=λqE(Y)。因此，基于医院的病人流量来估算最优床位规模，可以通过λ、q和E(Y)的估计值进行计算。

根据数量统计相关知识，很容易得出以下方法：

强度的估计λ ＾ =∑^T_iY_i/T (8)

λ ＾ 可以看作平均每天病人总数。转为住院病人的概率估计q ＾ = 住院病人数量 门急诊病人数量 (9)

q ＾ 可以看作是住院病人的数量占门、急诊病人数量的比例。

E(Y)的估计E(Y)＝Y － ＝ 1 m ∑^m₁Y_i (10)

Y － 表示住院病人的平均住院天数。因此，估算床位数为N ＾ =E[Z(1)]=λ ＾ ·q ＾ ·E(Y)。 (11)

基于深圳市和杭州市66家医院的抽查结果，根据实际床位数量，利用(8)和(11)式的结果进行床位估算测试，以实际床位规模大小，由低向高进行编号(表1)。

表1

表1(Table 1)

表1 实际床位数与估算床位数对照表 医院 编号 实际床位 数(N) 估算床位数 (N) ＾ 实际与估算差 (D=N-N ＾ ) 1 22 14 8 2 40 31 9 3 40 25 15 4 59 53 6 5 70 64 6 6 70 46 24 7 82 50 32 8 86 22 64 9 91 76 15 10 100 82 18 11 100 73 27 12 101 109 -8 13 103 64 39 14 104 101 3 15 150 175 -25 16 170 104 66 17 176 109 67 18 183 140 43 19 187 166 21 20 195 118 77 21 200 136 64 22 200 175 25 23 225 212 13 24 230 253 -23 25 232 198 34 26 250 194 56 27 310 300 10 28 320 258 62 29 320 222 98 30 346 267 79 31 400 514 -114 32 400 321 79 33 406 358 48 34 430 386 44 35 436 337 99 36 457 352 105 37 500 408 92 38 500 500 0 39 500 427 73 40 515 462 53 41 549 569 -20 42 600 375 225 43 600 429 171 44 612 515 97 45 648 564 84 46 660 488 172 47 700 590 110 48 725 650 75 49 734 552 182 50 800 831 -31 51 800 705 95 52 800 802 -2 53 800 878 -78 54 842 784 58 55 842 813 29 56 900 985 -85 57 910 938 -28 58 930 976 -46 59 986 1093 -107 60 987 1024 -37 61 1 050 975 75 62 1 100 1 094 6 63 1 157 1 358 -201 64 1 220 1 220 0 65 1 835 1 711 124 66 1 984 1 918 66

表1 实际床位数与估算床位数对照表

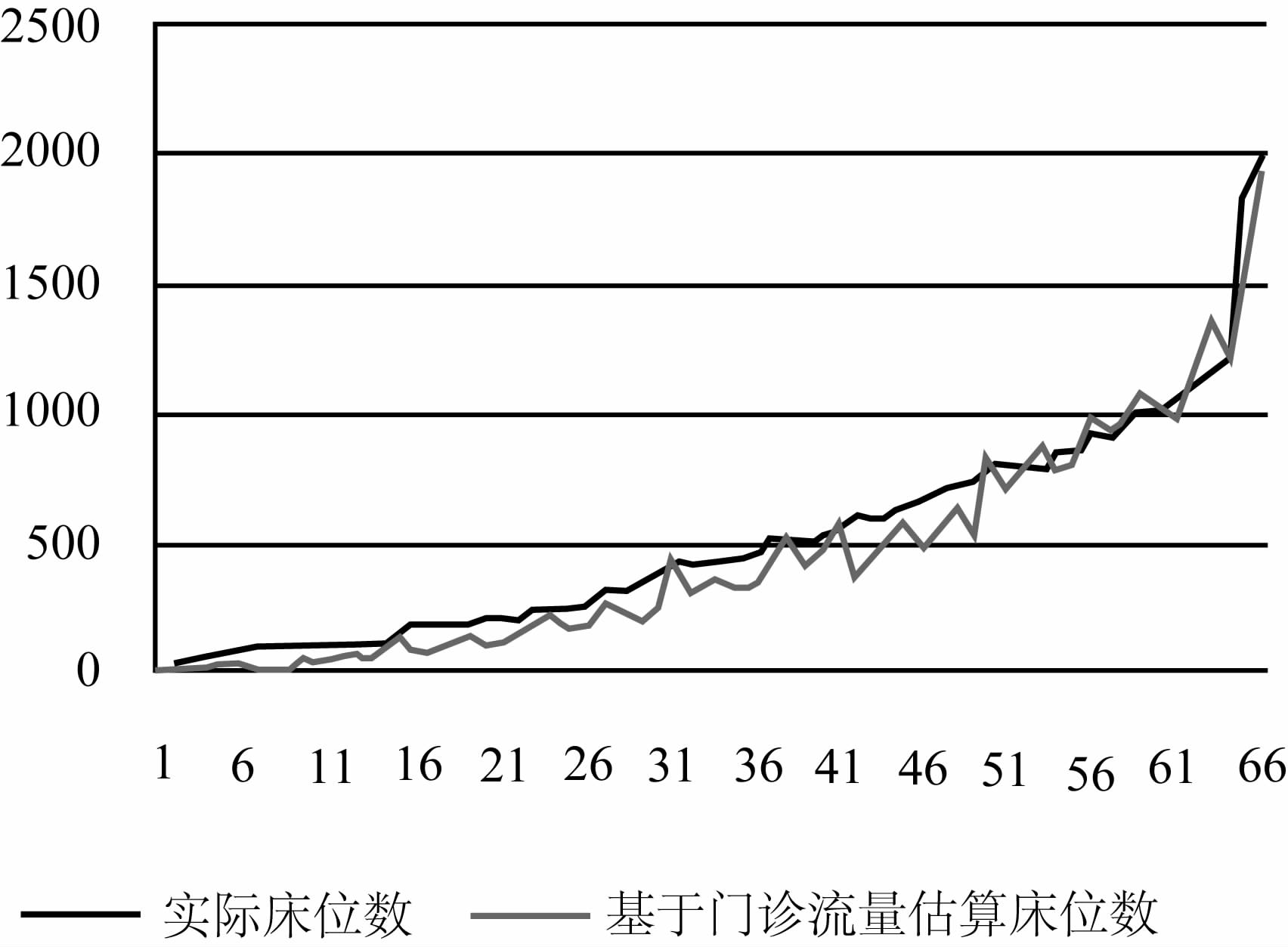
根据表1的数据，构造66家医院的实际床位数与估算床位数的对照图(图1)。由图1可以看 出，估算的床位数与实际床位数相差不大，直观上看拟合程度良好。

图1(Figure 1)

图1 实际床位数与估算床位数拟合曲线

显然由图1所示，实际数据与估算值拟合良好，但要判断实际床位数与估算床位数之间是否 存在显著性差异，需要进行假设检验。假定实际床位数量与估算床位数量的差D是随机波 动的，且假定D~N(μ,σ²)的正态分布。由于认为D是大样本的正态总体，且μ,σ²未知， 故采用t检验法，取显著性水平α=0.05，进行双边假设检验^[14]：

H₀∶D=0;

H₁∶D≠0

故选取统计量T= ｜D - ｜ S/ n ，(其中S为样本标准差，n=66)，很容易知道T服从t(65)分布。

根据表1数据计算知：n=66,S=285.599 37,D - =35.4242 42。由于 t=1.007 66＜t _{α 2} (65)=1.997，故接受原假设H₀。由此说明，我国的医院 基本上是以病人流量的大小来安排病床数量的，而且许多大型综合医院基本上没有闲置的病 床。所以，如果医疗资源不合理分配、大型综合医院的病人流量过大等问题得不到有效 解决，控制医院规模本身就是一个伪命题。