目前，卫生资源布局研究大多采用定性与定量相结合的方法，其中定量方法最为常见，如卫生资源/人口比值法等。^[1]但上述定量方法在应用时多以行政区划作为统计单位，规划单位过于粗放，行政区内部的资源布局无法得到细化分析，行政区的交界地带也容易出现规划的盲点。^{[2, 3]}随着地理信息系统(Geographic Information System,GIS)在卫生领域的应用，利用GIS平台将地理信息与卫生资源布局的测算相结合，可打破卫生资源调整中行政区划界限的阻碍，更有效地表达医疗资源的空间分布。目前卫生资源空间布局的研究主要聚焦于卫生资源的空间可达性方面，方法学的研制与应用也层出不穷，如引力法等。^[4]

引力法是将距离原理与牛顿万有引力定律相结合而衍生出的潜能模型，用以描述一物体对另一物体的空间作用。最初的引力法被用于比较区域中城镇吸引力的大小或者城市内部的土地利用、交通条件，比较发展的优势、劣势等。^[5]经过 Guagliardo、Joseph 等学者的研究，医疗资源空间可达性也有了应用较为广泛的引力法模型。^[6]引力法模型中有参数β即距离衰减系数，表示机构就诊概率与距离的衰减关系曲线的形状参数，β值越高，衰减越快。β值的大小受多种因素的影响，包括地理环境(郊区、市区、农村等)、活动类型以及目的地的类型等，甚至可以说针对每一种具体的供需关系都有一个具体的值。尽管学者们都认为实证研究(Empirical study)是确定β值的最好方法，但是校准β值所需的数据和信息通常是很难获得的，目前文献能检索到的实证研究很少。

距离是病人就诊的重要因素之一，对于同类别同级别的医疗机构，居民去某家医疗机构就诊的概率与距离成反比，不同居民点的病人到某家医疗机构就诊的比例也应与距离呈负相关关系，反映到实际中医疗机构的病人分布上，即在一定区域范围内，对于不同的居民点，该医疗机构的病人占各居民点人口的比例随着居民点与医疗机构的距离增加而下降。^[6]本研究通过分析上海市23家医疗机构的住院病人分布情况，找出住院病人概率和距离的函数关系，确定不同医疗机构住院病人距离衰减系数β，了解居民医疗服务获得的地理可及性现状，为区域卫生规划提供决策依据。

从上海市卫生信息中心获取上海市23家医疗机构2012—2013年的住院病人资料，其中二级医疗机构12家，三级医疗机构11 家。每家医疗机构随机抽取1 200名病人，共计27 600名。利用医院住院患者的地址信息，在谷歌地图中获取病人常住地址经纬度，确定有效地址26 248例，有效率为95.10%，形成住院病人常住地址地理信息数据库。

全部数据采用 EXCEL 2007录入建库，利用GIS软件计算就诊距离以及住院病人概率，应用 SAS9.2统计软件进行曲线模型拟合。

第一步：将数据以excel形式导入GIS中，并计算住院病人到就诊医疗机构的点距离。

第二步：以医疗机构为圆心，半径为R_i=2(不同医疗机构i不同，因为各医疗机构具体位置不同，研究范围是整个上海市,i最小为35，最大为47)建多重缓冲区，形成了以医疗机构为中心的i个环带(靠近中心的环带为圆)(图1)，各环带距离医疗机构的距离为r_i，r_i可按下式计算。^[8]

图1(Figure 1)

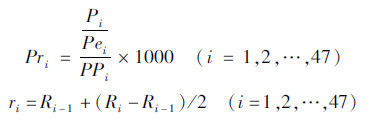
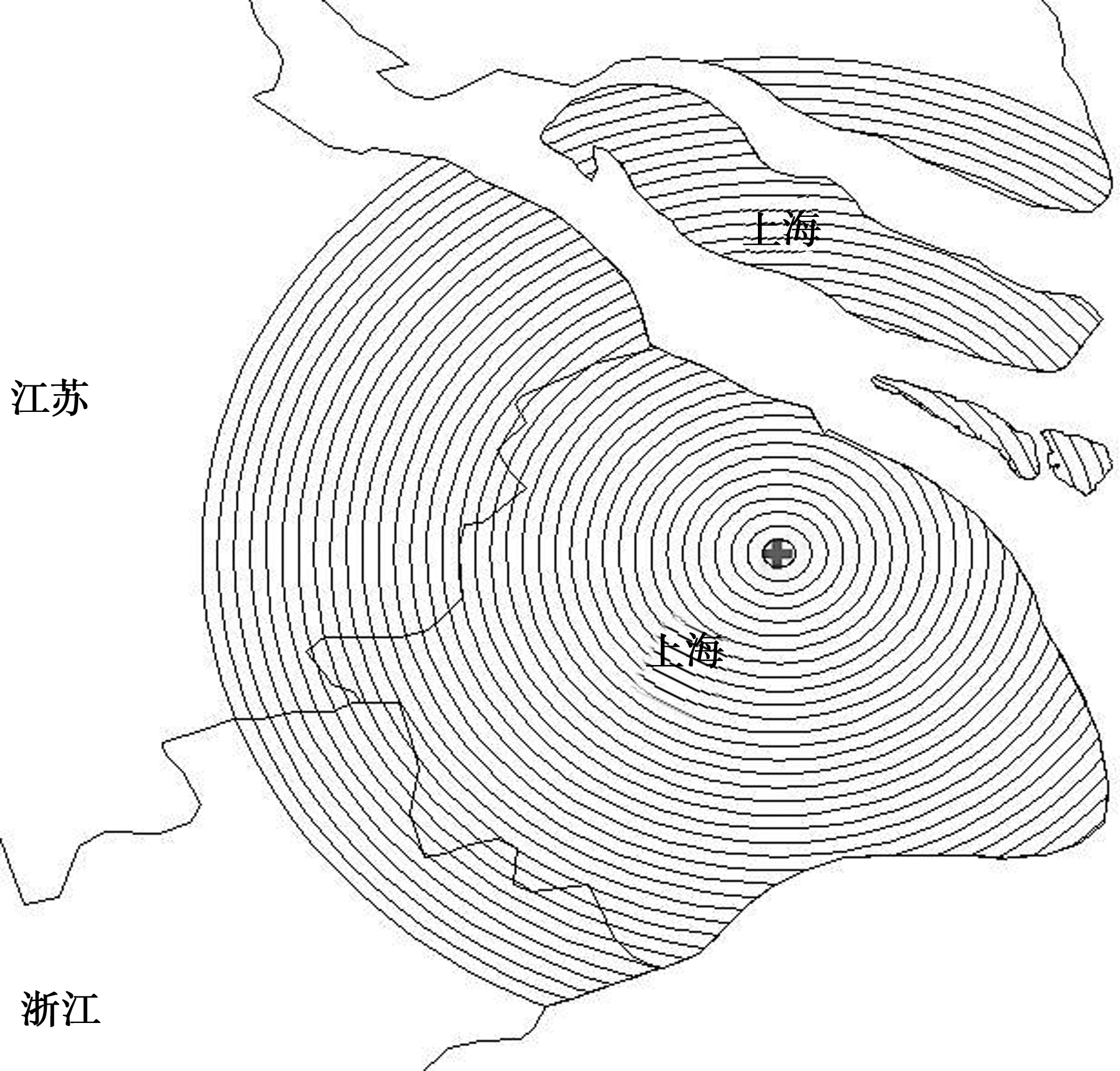
图1 上海市F医院多重缓冲区

第三步：计算住院病人概率(Pr_i)，计算如下：

Pr_i代表住院病人环带i的住院病人概率，P_i代表环带i的住院病人频数，Pe_i为抽样比例，即抽取样本中有效地址住院病人数除以医疗机构总的住院病人数。PP_i代表环带i所有居民人口数,即环带内上海居民人数与涉及到江苏、浙江地区人口数总和。环带内的上海居民人数可以计算栅格化的居民点，每个居民点有相应的人数，最后加总得到各环带上海市居民人数。江苏、浙江地区涉及到南通、无锡、苏州、嘉兴、湖州五市，查询这五市的总人口和总面积，计算出平均的人口密度。通过GIS裁剪出环带内江苏、浙江的面积，乘以人口密度，得出环带内江苏、浙江的人口数。两者相加，得出环带内总人数。

按照上述三个步骤分别计算出23家医疗机构的住院病人概率，下面以上海市F医院为例(表1)。

表1

表1(Table 1)

表1 上海市F医院住院病人概率与距离的数据矩阵 数据点 Ri ri Pi Pri 1 2 1 257 2.107 1 2 4 3 205 0.506 5 3 6 5 179 0.396 5 4 8 7 176 0.377 7 5 10 9 121 0.265 8 6 12 11 74 0.170 5 7 14 13 56 0.165 1 8 16 15 32 0.104 4 9 18 17 10 0.037 1 10 20 19 7 0.029 8 11 22 21 5 0.022 4 12 24 23 2 0.010 2 13 26 25 5 0.025 0 14 28 27 3 0.017 6 15 30 29 2 0.012 6 16 34 33 1 0.007 0 17 36 35 1 0.008 4 18 40 39 1 0.008 6 19 46 45 1 0.010 0 20 48 47 1 0.010 8 21 50 49 2 0.024 7 22 52 51 1 0.013 1 23 58 57 1 0.012 1 24 70 69 1 0.011 3

表1 上海市F医院住院病人概率与距离的数据矩阵

第四步：进行曲线模型拟合，曲线模型拟合借鉴距离衰减方程，采用非线性回归法对23家医疗机构进行多种曲线模型模拟。^[9]

首先，对常见的线性模型、指数曲线模型、对数曲线模型和乘幂曲线模型4种基本距离衰减函数进行拟合,然后,对一种结构相对复杂的距离衰减函数,即平方指数曲线模型进行拟合^{[10, 11, 12]}。其中，P_r是到医疗机构距离为r处的住院病人概率，a为常数，β为距离衰减系数。住院病人概率随距离增加而衰减，因此β为负值。拟合结果以F医院为例，其指数曲线模型、乘幂曲线模型的决定系数较好，都在0.90以上(表2，图2)。

表2

表2(Table 2)

表2 上海市F医院住院病人空间分布模型的回归及拟合结果 模型 一般表达式 a β R2 线性回归 线性模型 Pr=a-βr 0.50 0.01 0.25 非线性回归 对数曲线模型 Pr=a-βInr 1.21 0.35 0.67 (迭代法) 指数曲线模型 Pr=ae-βr 3.31 0.48 0.94 乘幂曲线模型 Pr=ar-β 2.10 1.12 0.99 平方指数曲线模型 Pr=ae-βr2 2.45 0.16 0.90

表2 上海市F医院住院病人空间分布模型的回归及拟合结果

图2(Figure 2)

图2 上海市F医院住院病人概率曲线拟合图

从表3可知，除了F医院，其它22家医疗机构指数曲线模型、乘幂曲线模型的决定系数整体都较好，指数曲线模型、乘幂曲线模型对23家医疗机构的住院病人分布都较有普适性。

表3

表3(Table 3)

表3 23家医疗机构指数曲线模型、乘幂曲线模型拟合结果 医疗机构 等级性质 指数曲线模型 乘幂曲线模型 a β R2 a β R2 A医院 二级综合 15.43 1.29 0.99 4.26 2.32 0.99 B医院 二级综合 25.54 0.36 0.99 18.26 1.05 0.94 C医院 二级综合 27.38 0.70 0.99 13.71 1.39 0.99 D医院 二级综合 4.17 0.53 0.99 2.50 1.24 0.99 E医院 二级综合 14.73 0.27 0.96 12.06 0.95 0.94 F医院 二级综合 3.31 0.48 0.94 2.10 1.12 0.99 G医院 二级综合 0.75 0.38 0.94 0.54 1.01 0.98 H医院 二级综合 50.54 0.35 0.99 36.74 1.05 0.93 I医院 二级综合 10.94 0.57 0.99 6.23 1.33 0.98 J医院 二级综合 37.8 0.13 0.88 35.62 0.69 0.66 K医院 二级专科 2.83 0.85 0.97 1.21 1.45 0.99 L医院 二级专科 19.09 0.15 0.98 18.74 0.74 0.84 M医院 三级综合 27.63 0.59 0.96 15.42 1.18 0.99 N医院 三级综合 20.12 0.46 0.95 13.12 1.09 0.99 O医院 三级综合 7.99 0.19 0.77 7.60 0.72 0.97 P医院 三级综合 9.48 0.21 0.61 8.64 0.70 0.87 Q医院 三级综合 8.73 0.12 0.85 9.08 0.64 0.90 R医院 三级综合 1.16 0.10 0.72 1.32 0.60 0.85 S医院 三级综合 70.02 0.20 0.92 66.47 0.89 0.92 T医院 三级综合 25.73 0.50 0.97 15.84 1.15 0.99 U医院 三级综合 10.82 0.11 0.83 9.88 0.61 0.53 V医院 三级专科 3.25 0.08 0.93 3.89 0.57 0.89 W医院 三级专科 1.13 0.03 0.35 2.08 0.49 0.69

表3 23家医疗机构指数曲线模型、乘幂曲线模型拟合结果

指数曲线模型中，二级医疗机构住院病人距离衰减系数平均为0.51，最小值为0.13，最大值为1.29，置信区间为[0.30，0.71]，其中，综合医疗机构住院病人距离衰减系数平均为0.51，专科医疗机构住院病人距离衰减系数平均为0.50；三级医疗机构住院病人距离衰减系数平均为0.23，最小值为0.03，最大值为0.59，置信区间为[0.11，0.36]，其中，综合医疗机构住院病人距离衰减系数平均为0.27，专科医疗机构住院病人距离衰减系数平均为0.05。

乘幂曲线模型中，二级医疗机构住院病人距离衰减系数平均为1.19，最小值为0.69，最大值为2.32，置信区间为[0.92，1.47]，其中，综合医疗机构住院病人距离衰减系数平均为1.21，专科医疗机构住院病人距离衰减系数平均为1.09。三级医疗机构住院病人距离衰减系数平均为0.78，最小值为0.49，最大值为1.18，置信区间为[0.61，0.96]，其中，综合医疗机构住院病人距离衰减系数平均为0.84，专科医疗机构住院病人距离衰减系数平均为0.53。

从23家医疗机构模拟结果的决定系数来看，二级医疗机构中指数曲线模型和乘幂曲线模型结果拟合整体较好，但是指数曲线模型决定系数相对较高。三级医疗机构中乘幂曲线的决定系数相对于指数曲线模型较高。指数曲线适用于速度增减越来越快的数据值，乘幂曲线是一种适用于以特定速度增加的数据集的曲线。三级医疗机构的住院病人衰减的趋势因其专科、软硬件设施等要相对平缓，二级医疗机构往往是区域性医疗机构，其住院病人衰减趋势相对于三级医疗机构速度更快。因此，二级医疗机构住院病人分布推荐采用指数曲线模型；三级医疗机构住院病人分布推荐采用乘幂曲线模型。

在指数曲线模型中，二级医疗机构的住院病人距离衰减系数均值(0.51)大于三级医疗机构(0.23)；二级医疗机构中综合医疗机构住院病人距离衰减系数均值(0.51)与专科医疗机构(0.50)相差不大，这可能与二级医疗机构常常作为区域性中心，服务于特定的区域有关；三级医疗机构中综合医疗机构住院病人距离衰减系数均值(0.27)大于专科医疗机构(0.05)。在乘幂曲线模型中，二级医疗机构的住院病人距离衰减系数均值(1.19)大于三级医疗机构(0.78)；二级医疗机构中综合医疗机构住院病人距离衰减系数均值(1.21)大于专科医疗机构(1.09)；三级医疗机构中综合医疗机构住院病人距离衰减系数均值(0.84)大于专科医疗机构(0.53)。二级医疗机构的住院病人概率随距离衰减的趋势快于三级医疗机构，综合医疗机构的住院病人概率随距离衰减的趋势快于专科医疗机构。医疗机构的等级和性质是人们就医选择的重要影响因素。这与之前的相关研究结果一致。^{[7, 12, 13, 14, 15]}

曲线模型拟合采用的是非线性回归法，非线性回归直接基于概率值而不是概率值的对数，其回归残差平方和较小。因为考虑的是绝对误差，高概率地区的误差(绝对误差)值限制在一个数据范围内。因此，住院病人的总数估计值常常比线性回归的结果更接近现实值，但低概率地区的概率估计值会存在较大的相对偏差。^[16]

(1)指数曲线模型、乘幂曲线模型研究23家医疗机构住院病人分布具有普适性。研究二级医疗机构中住院病人分布选择指数曲线模型更为适合，三级医疗机构中住院病人分布选择乘幂曲线更为适合。

(2)从医疗机构等级来看，无论是住院病人分布的指数曲线模型还是乘幂曲线模型，二级医疗机构的决定系数均大于三级医疗机构，三级医疗机构的β较小，住院病人概率递减较慢；二级医疗机构的β较大，住院病人概率递减较快。从医疗机构性质来看，无论是二级医疗机构还是三级医疗机构，专科医疗机构的距离衰减系数都低于综合医疗机构，专科医疗机构的β较小，住院病人概率递减较慢；综合医疗机构的β较大，住院病人概率递减较快。这证明了在影响居民选择医疗机构的各种因素中，医疗机构的等级和性质尤为重要，对于拥有更高等级或优势专科的医疗机构，病人愿意经历更长的距离、花更多的时间获得该医疗服务。因此在衡量居民医疗服务获得的地理可及程度时，需要针对不同等级、不同性质的医疗机构确定距离衰减系数。

在区域卫生规划中，卫生资源配置水平的计算往往采取服务区域法，即将卫生资源/人口比值法和距离因素相结合，在就近医疗的原则下将区域按照医疗机构位置进行划分，测算每个划分区域里的卫生资源/人口比值，以确定该服务区域内的资源配置水平。但这仅适合对医疗水平相似的医疗机构卫生资源配置水平进行研究。对于一个特定的区域内拥有不同等级的医疗机构，引力法可以计算出每个居民点的卫生资源配置水平，不足在于所涉及的距离衰减系数不易确定，需进行调查抽样。随着数据的不断完善和GIS技术在卫生领域的应用，引力法中不同级别、类别的距离衰减系数将逐步得以确定。因此，在制定区域卫生规划时，应将引力法纳入其中，对于不同级别、类别的医疗机构应采用不同的距离衰减系数，以便科学地计算出区域中卫生资源的配置水平，为区域卫生规划决策提供科学依据。