2. 上海市医保办公室 上海 200125;
3. 上海健康信息协同研究中心 上海 200041
2. Shanghai Medical Insurance Bureau, Shanghai 200125, China;
3. Shanghai Health Information Center, Shanghai 200041, China
近年来,随着国民经济的不断发展和医疗技术的显著提高,居民对现代医疗服务的需求不断提升。其中,参保人员要求医保药品能够就近获得;与此同时,由于区域间人口密集程度、定点药店位置与数量、交通路网建设状况等多种因素的不同质,使得不同区域间的居民对于医保药品的需求与利用情况差异显著。以上两点均对新医保定点药店规划提出了高要求。定点药店规划作为一种引导医保药品服务供给和空间配置的重要手段,其原有的基于自然区域界线或者行政区划界限的药店规划及管理模式已无法满足现状的需要。因此,本研究以公平和效率为导向,本着充分发挥医保资金作用的原则,对区域内药店实现全方位、针对性与精确性的规划。为实现这一目标,应探讨出一种针对规划地域范围内的基层药事服务圈的界定、划分和可视化表达方法。
2 研究方法 2.1 基层药事服务圈的界定标准及划分方式“居民步行15分钟能够获得医疗服务或药品”已成为我国卫生领域内的共识。世界卫生组织(WHO)将居民每步行15分钟可以获得医疗服务或药品作为保障人群基本健康的目标;国内多地自2016年起开始提出构建15分钟生活圈目标,即实现社区公共服务设施15分钟步行可达覆盖率100%等。以这些文件为依据,切合定点药店规划“让人民群众更为便捷地获得医保药品”的目标,可将居民步行15分钟到达一所定点药店并有效获得医保药品作为定点药店规划的最终目标,即按照居民15分钟步行路网距离的可及范围作为基层药事服务圈的界定标准。划分方式多样,研究为保证公平和效率,采用了基于网格化管理思想的区域划分方法:即将规划地域范围作为一个整体,借助地理信息系统对空间的划分、空间数据的获取、组织与管理等功能,按照一定的标准将连续的工作区域的平面空间离散化[1],并在以网格为单元的计算环境下,对空间信息资源包括药店、人口、交通等信息,进行一体化整合、组织与管理。该方式有助于规划者在小范围内实现对每家药店的精细化管理,明确所需管理的对象,为药店定点规划提供一种全新的思路与方式。
2.2 基层药事服务圈界定及可视化表达操作步骤本研究根据规划目标,运用地理信息系统ArcGIS10.0软件,按照“15分钟步行路程(图 1,高斯距离值为1 500米,即AB+AC=1 500米,转换成六边形半径r=BC为1 060.82米)”为基准长度对需要定点药店规划的地域空间进行切割处理,形成多个六边形,而每一个六边形则被认为是一个“居民15分钟步行区域”,即基层药事服务圈,也可称为规划管理的一个基本单元。其同时符合:(1) 相邻的网格单元间彼此邻接但不重合或交叉;(2) 易于将数据按照需要进行不同分辨率的空间化,使空间关系可清晰表达;(3) 形状呈面状、规则状;(4) 不同时间所采集的数据信息在空间上具有可比性。这些特点均为定点药店规划提供了良好的先决条件。并且,当网格一经划定并覆盖至整个地域范围后,每个网格的设定及其所含有的药店、人口、交通等信息数据便固定下来。具体操作步骤为:第一步,运用ArcGIS工具箱中的鱼网工具生成网格:点击ArcToolbox→选择数据管理工具→要素类→创建鱼网(输入网格所需的像元高度与宽度, 选中:创建标注点)→确定,生成以单位正方形鱼网网格以及鱼网中心点点图层;第二步,复制鱼网中心点点图层→将复制的点图层移动至原鱼网中心点点图层的对角中心位置上(建议以正方形鱼网网格作为参考标尺)→合并原点图层与移动点图层,将合并后的鱼网点图层作为泰森多边形的中心点;第三步,生成泰森多边形:点击ArcToolbox→Analysis tools→邻域分析→创建泰森多边形,输入合并后的点图层,生成以六边形为单位的规则格网图层;最后,规划地域范围的内六边形规则网格图层可通过裁剪工具获得:点击ArcToolbox→选择分析工具→提取→裁剪,输入要素设为泰森多边形图层,裁剪要素设为规划区域行政区划图层,输出结果即为所规划境内居民15分钟步行区域六边形规则格网图层,或称基层药事服务圈图层。

|
图 1 基层药事服务圈图 |
对于基层药事服务圈形状的选取上,课题组经过多方考虑,最终采用的是正六边形规则形状的单元网格。事实上,网格作为一种间接的空间参照体系,可根据具体的规划需要而人为的进行形状调整。总体来说,网格可分为规则网格和不规则网格,其中规则网格形状分为圆形、正方形等。由于规则网格是空间数据处理中常用的建模方式[2],可将空间信息表示成一系列按行与列排列的同一大小的网格单元,使得参照体系具有较高的标准化程度, 并可将误差控制在网格单元的范围内[3]。故研究着重探讨了选取规则网格中的何种形状用以最佳地表达药店的服务区域:(1) 如何实现地域范围内无缝全覆盖;(2) 兼顾药店的服务区域范围的有效表达。研究首先对2种基本形状的网格划分方法进行了比较。
3.1 圆形网格为合理表达某地的服务范围,传统上规划采用“服务半径”概念,即圆形形状作为可视化表达的工具。但如果沿用圆形作为分割地域范围的基本形状,则会出现无论将圆形相交或相离,都无法实现对于区域的完全无缝覆盖(图 2)。同时,研究发现若将圆形相交,同时将所相交的部分面积尽量减小,即以圆心为顶点进行两两连接,可得边长为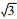
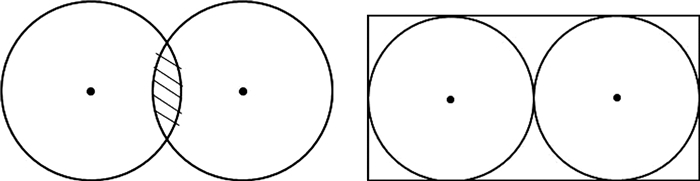
|
图 2 圆形网格图 |
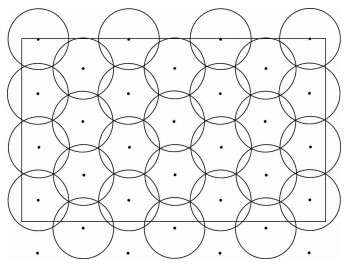
|
图 3 圆形相交网格图 |
传统的正方形网格是最有效的分割区域单元的形状,网格边长为外接圆半径,可实现对地域范围内无缝全覆盖(图 4)。但正方形却无法很好的表示药店的服务区域,体现不出圆形所表示的覆盖面积特征,即未能说明一家药店具体的服务覆盖范围。
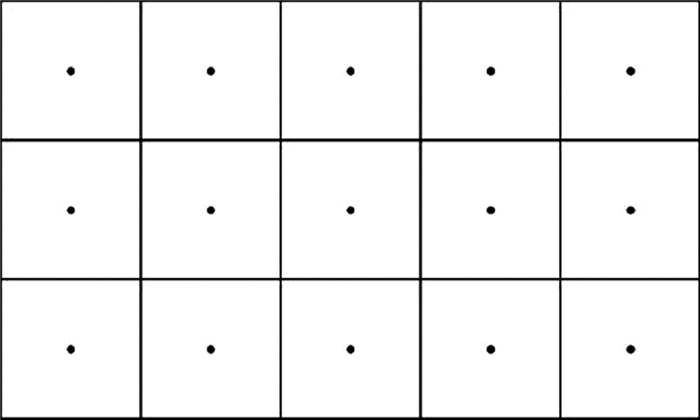
|
图 4 正方形网格图 |
基于上述探讨,服务区域的可视化表达图形是圆形,但由于圆形本身具有的特性使其无法实现均匀且无重复的切割空间,而正方形虽可以有效切割空间,但在表达服务区域方面有所欠缺。为克服两者的缺点,汲取其可利用的特性,将圆形两两相交、将相交部分减至最小,并同时进行简化:即用构成正方形边长的直线线段代替圆形弧线,用圆形的内接正六边形来替代圆形,此时六边形半径为d2(图 5)。
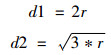
|
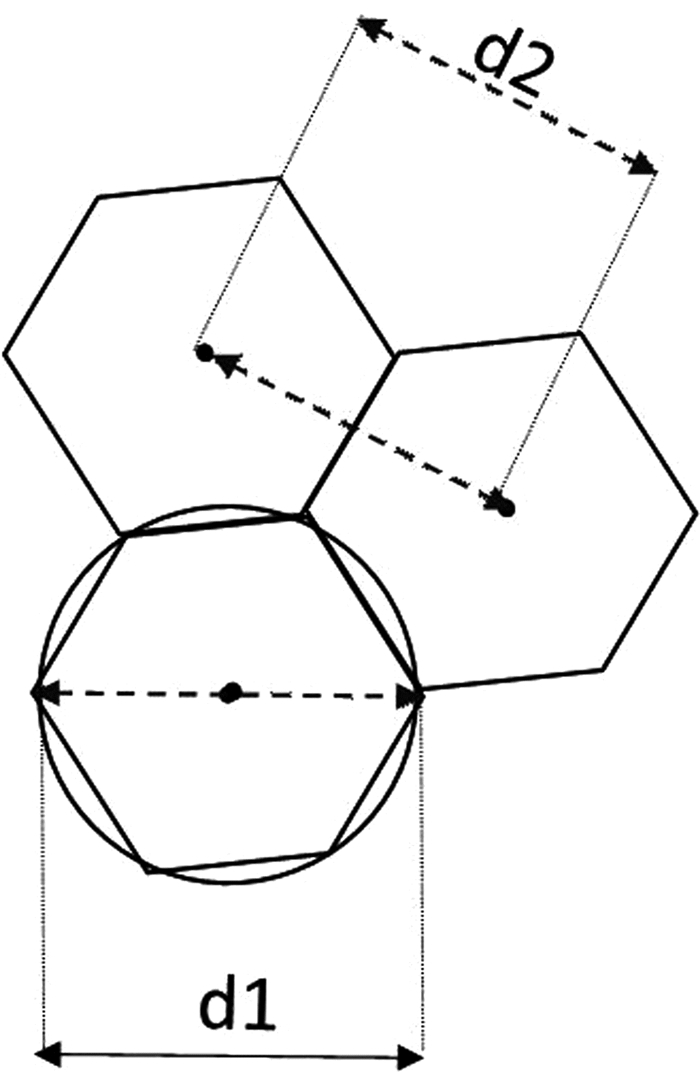
|
图 5 六边形网格图 |
正六边形这种形状接近圆形的理想服务覆盖区域,同时也满足六边形两两之间无缝隙也无重叠部分, 可避免出现对对象的重复或遗漏管理。达到医保定点药店规划服务区域划分的基本要求(图 6)。同时,若管理方需要提高对每家药店的高效管理,也可对每个六边形网格进行基于实际地理位置的地理编码。从而实现真实地理空间位置与所画网格之间的双向互查。
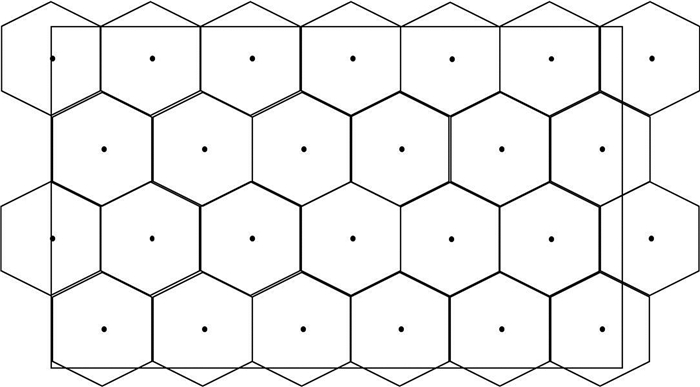
|
图 6 六边形网格区域规划图 |
本研究所探讨的方法学信度与效度分析采用模拟操作及验证方法。具体如下:以某市为例,原始数据采用某市道路交通路网数据库,数据库来源于某市测绘院,包含某市所有区县及乡镇街道的行政边界图,数据来源于2015年。研究按照居民15分钟步行距离为标准,应用地理信息系统软件,对区域进行基层药事服务圈的界定、划分和可视化表达,即将某市按照15分钟步行可及范围地图化,从而绘制某市15分钟的基层药事服务圈(图 7)。绘制思路如下:按照标准可知,居民15分钟步行的高斯距离为1 500米,即转换成基层药事服务圈的六边形网格半径则为1 060米,则每个基层药事服务圈的面积S六边形=3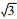
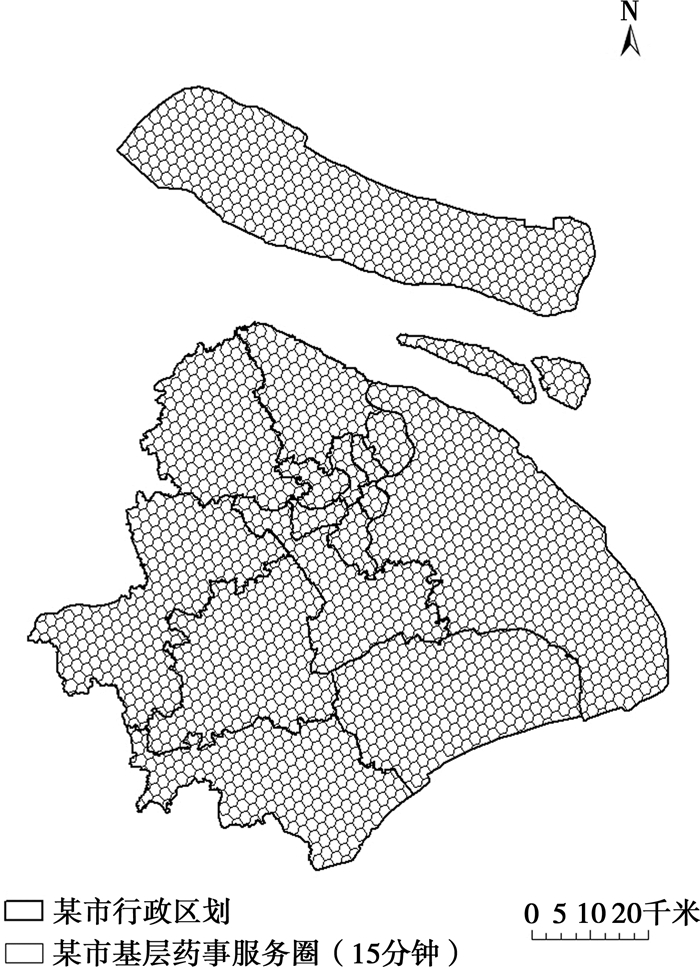
|
图 7 某市2 188个15分钟基层药事服务圈(六边形)图示 |
上述实例中的标准是以居民15分钟步行达到一所医保药店为标准进行的基层药事服务圈划分。但随着居民医疗资源需求的逐步上升,规划也可将标准予以适当提高,如以10分钟步行距离作为基层药事服务圈的标准。研究采用同样的原始数据,按照居民10分钟步行距离为标准,利用地理信息系统软件, 对区域进行基层药事服务圈的界定、划分和可视化表达,即将某市按照10分钟步行可及范围地图化,从而绘制某市10分钟的基层药事服务圈(图 8)。绘制思路如下:按照标准可知,居民10分钟步行的高斯距离为1 000米,即转换成基层药事服务圈的六边形网格半径则为707米,则每个基层药事服务圈的面积S六边形=3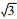
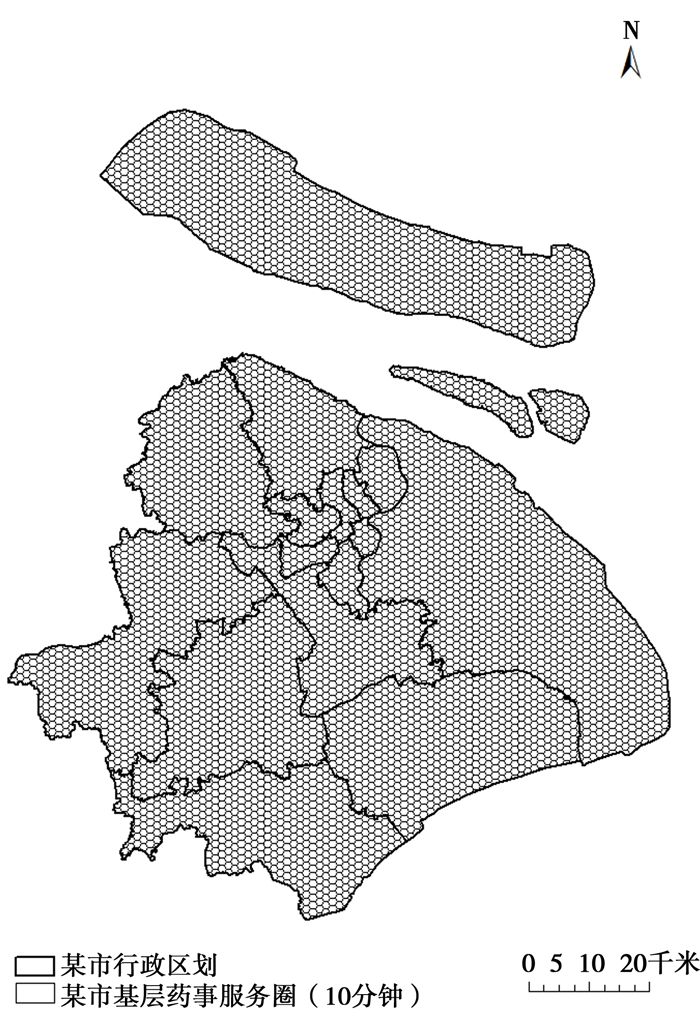
|
图 8 某市5 941个10分钟基层药事服务圈(六边形)图示 |
上述操作均由有多年规划积累经验的课题组操作。同时,在方法学的研制过程中还由非常熟悉该领域的医保办行政人员与医保局事务中心的各专家共同参与商讨;所得结果也经过了来自各区县各级医疗机构、国营连锁药店、民营连锁药店、中医中药销售药店、个体药店以及医保定点药店联合工作组的多方专家论证,且已被具体应用于某市定点零售药店发展规划(2017—2020) 中,被某市医疗保险局采纳。综上所述,可认为本研究所研制的方法学具有较高的可靠性和确实性。
5 小结本文主要探讨的是基于网格化管理思想,以公平和效率为导向的基层药事服务圈界定和可视化表达方法,可为定点药店规划提供一种全新的思路与方式。当然,本研究的操作方法并非局限于基层药事服务圈的划分上,也可应用于任何地域范围内一定标准下的基层公共服务供给或公共资源配置的服务圈划分。本研究方法由于研究借助了网格化管理思想,并基于地理信息系统,对基础数据的处理方式突破了传统的粗放型规划方法,不再受行政区划或乡镇街道划分等的限制,不但可保证规划的公平和效率,同时也使规划达到了全方位、精确性、针对性管理对象的目标,值得推广。
然而,方法学也存在一定的局限性。由于是将规划区域绘制成可覆盖全区域的连续性图层,那么将有可能出现需规划的对象距离较近但却正好处在两个基层服务圈内的现象。但由于规划是基于单位均匀网格的针对性管理,因此,容易造成规划最终所纳入的管理对象距离过近的问题,违背了规划以实现资源配置公平与效率的初衷。针对该问题,课题组会进行后续研究。
| [1] | 廖书标. 地理网格在城市管理信息系统中的应用研究[D]. 长沙: 中南大学, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10533-2009240744.htm |
| [2] | 李琦, 罗志清, 郝力, 等. 基于不规则网格的城市管理网格体系与地理编码[J]. 武汉大学学报(信息科学版), 2005, 30(5): 408–411. |
| [3] | 地理网格[EB/OL]. http://baike.baidu.com/link?url=nSF7O54JKOZOOoqk24l7bwhXppC0IcRKuyA9sn6_SBW1-xo5eYKdp5FR88z3nb7YJdQGkezHXsylmzy3x0Rm-WWYW2ot8FM6d4i8casl6M8y6b4S0MCHFbkZdtytMCZX |
(编辑 赵晓娟)





