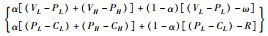2. 邢台市第九医院(巨鹿县医院) 河北邢台 055250
2. Xingtai Ninth Hospital(Jvlu County hospital), Xingtai Hebei 055250, China
在中国深入推进医疗卫生体制改革进程中,医疗卫生服务体系的离散化与碎片化、医疗卫生体制改革困难重重、公立医院利益导向且管理无序等问题凸显。[1]深化医改促进中国卫生资源总量大幅提升,每千人床位数和每千人卫生人员数基本持平于美国水平。然而,与美国逐年下降的入院次数、平均住院日和病床使用率不同,中国门诊服务利用不足,住院服务被过度依赖的现象较为严重。[2]究其原因,经济水平的提高加剧了需求侧对优质医疗服务的需求和利用、对医疗效果的过高期望、对三级医院的迷信,形成了需求侧对三甲医院住院服务的过度需求;在此客观医疗需求扩张下,加之医方主观的“利益”驱动,强烈刺激供给侧拥有优质医疗资源的三级医院无序扩张床位数,最终导致医疗资源配置的“倒金字塔”;不仅如此,以“疾病”为核心的医疗服务模式也加剧了“重治疗、轻预防,重医院、轻基层,重住院、轻门诊”程度。需求侧就医行为的错位、混乱、无序、过度依赖三级医院住院服务与供给侧医疗卫生资源的不合理与低效率利用,使得有必要对二、三级医院医疗资源进行纵向整合,形成医疗服务提供体系协调均衡发展。[3, 4]
在优质医疗资源整合方面,有研究对北京市优质医疗资源进行功能疏解分析,指出应依据市场需求进行医疗资源的规划配置,加强区县医院的建设以做好优质医疗资源功能疏解的承接工作。[5]一项对上海市住院病人的跨区域流动实证分析指出,优质医疗资源对住院病人的跨区域流动具有虹吸作用。[6]另一项研究则分析了辽宁省和全国住院患者分流前后经济效益差,提出各级医疗机构间加强资源整合的相关建议。[7]也有研究从功能协同的角度对青岛卫生系统进行了系统设计。[8]有学者研究了患者就医行为的住院选择结果的最佳预测模型[9],并基于MO2TOS算法进行分级诊疗模式下北京市住院患者流预测分析[10]。
在应用博弈解决医疗问题方面,有研究制定了基于政府、公立医院、患者、药品医疗器械商等利益相关者间博弈分析的相关公立医院利益补偿制度。[11]另有研究勾画了公立医院及其利益相关者的演化博弈路径[12];有研究构建了医保基金、患者、上级下级医院的三阶段动态博弈模型,表明应合理利用医保支付杠杆来完善分级诊疗制度[13];还有研究分析了远程医疗合作背景下社区医院和患者的策略选择博弈[14];以及医院与患者对医疗APP的选择行为[15]。
上述关于优质医疗资源整合的文献多是基于某一地区的实证研究,博弈在医疗领域的应用研究则多为特定背景或因素下的利益相关者行为分析,较少从二三级医院顺次就诊整体流程方面研究患者和医生间的交互行为。基于此,本研究建立了患者首诊与二三级医院医生诊疗策略的演化博弈理论模型,分析了影响患者首诊二级医院与二三级医院医生分级诊疗策略的主要影响因素,并据此提出分级诊疗制度下促进二三级医院服务资源协同发展的建议。
2 模型假设假设患者和医生均为自利、风险中性、效用最大化群体。患者群体因出现身体上的某种不适而需要就医。其问题可以分为两类:复杂型多发病M和疑难重症m,对应的患者群体类别为:P={A, B},A对应复杂型多发病M,所占比例为θ;B对应疑难重症m,比例为:θ=1-θ。鉴于复杂型多发病与疑难重症的界限模糊,临床表现较为相似,因而患者通常能够意识到病症的存在,但不能确定所患疾病的类型,需要依靠知识渊博、临床经验丰富的医生为其提供诊断和治疗服务。然而,患者多年形成的就医习惯促使经济状况良好、三级医院可及性好的城市患者首诊三级医院情况普遍;而受家庭经济收入影响的农村患者则多习惯“小病抗,大病拖”,病情恶化不得已才去二级医院就诊,此时二级医院已无力作为,长此以往农村患者便形成首诊绕开二级医院直接去三级医院的就医习惯。[16]鉴于该情况,假设患者可根据自我感知病情的严重程度及其相关就医经验自主决定去哪一级别医院接受医疗服务。
医院分为两类:二级医院L(包括县医院、县级市医院、部分市医院)和三级医院H(包括专科医院、三级综合医院),对应的医院类别为:I={L, H},其中二级医院L所占比例为γ;三级医院H所占比例①为:γ=1-γ。医生的策略有两类:常规诊疗策略(Ⅰ)和分级诊疗(Ⅱ)策略。常规诊疗策略指患者到达某二级(三级)医院,该院医生做出诊断及继续在该院治疗或需上转至三级医院治疗(继续在该院治疗)的建议。若需转院,则患者自主离开二级医院,再选择进入三级医院;分级诊疗策略是指患者到达某二级(三级)医院,该院医生做出诊断及继续在该院治疗或需上转至三级医院治疗(继续在该院治疗或可下转至二级医院治疗)的建议,若需转院,则患者进入该三级医院(二级医院)的转诊绿色通道,等待转诊至三级(二级)医院。
① 文中不考虑医院比例对医生就医决策的影响。假设医生群体通过加班和其他调度方式来使得进入该医疗机构的患者所需的医疗服务均得到满足。
鉴于现实情况中二级医院和三级医院的服务水平具有差异性,为简化模型,假设复杂型多发病在二级医院和三级医院均可得到较好的诊断治疗,疑难重症则必须到三级医院才能得到较好的诊断治疗。
2.1 构建博弈支付矩阵假设复杂型多发病M患者A在二级医院L接受诊断并治疗后,身体康复的效用为VL;疑难重症m患者B在三级医院H接受诊断并治疗后,身体康复的效用为VH(考虑疑难重症的诊疗难度较高,身体康复对患者的影响较大,因而效用值更高,即有VH>VL);患者B在二级医院接受常规诊疗后,再进入三级医院接受诊疗的概率为α,(α∈(0, 1));患者A在三级医院接受医疗服务所获得的效用为其在二级医院的效用的δ倍(考虑三级医院医疗设备先进性、治疗环境舒适性及诊疗权威性,即有δ≥1);二级医院与三级医院诊疗费用分别为PL与PH,(PH>PL,三级医院的诊疗费用较二级医院高);二级医院与三级医院的诊疗成本分别为CL与CH,(CH>CL,三级医院的诊疗成本较二级医院的高,但其差值小于诊疗费用之差值,即PH-PL>CH-CL);患者B选择二级医院L,二级医院因服务水平有限而未能彻底治愈患者,给患者带来的效用损失为ω;二级医院由此带来的声誉损失为R;患者B在三级医院诊疗后,身体康复为三级医院带来的声誉增加为ΔR(考虑患者风险规避的心理因素,因而病情未能彻底救治所带来的声誉损失要大于疑难重症及时救治的声誉增加,即R>ΔR);分级诊疗策略下,患者经由二级医院上转至三级医院或经由三级医院下转至二级医院向首诊医院支付的费用为P;首诊医院支付的诊断费用为C。
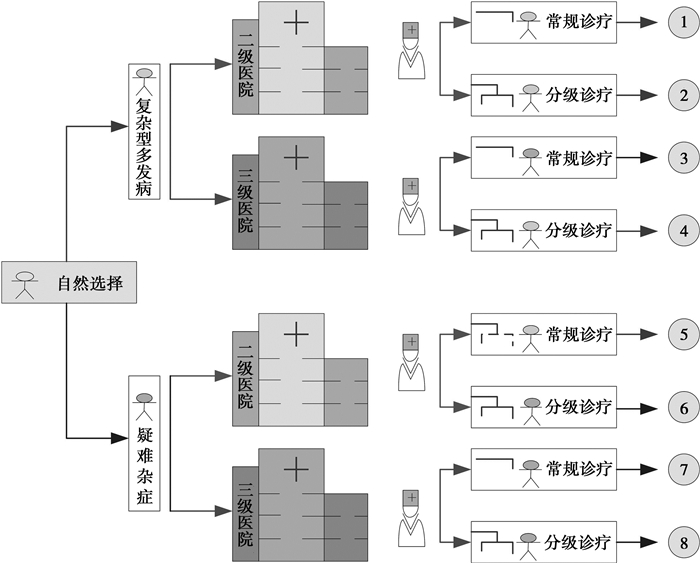
基于上述模型假设及分析,构建患者就医选择博弈的三阶段模型,其中患者具有先动优势。第一阶段自然选择患者所患问题类型;第二阶段患者根据自我患病感知情况选择进入二级医院或三级医院,进入二级医院的概率为p,进入三级医院的概率为p=1-p;第三阶段医生群体观测到患者的策略但不确切知道患者的类型,选择常规诊疗或分级诊疗,其中选择分级诊疗的概率为q,选择常规诊疗的概率为q=1-q。图 1显示了不完全信息下患者和医生决策路径扩展式表述,表 1为相关收益表,据此构建患者首诊决策与医生诊疗策略的博弈支付矩阵见表 2。
|
图 1 不完全信息下患者和医生决策路径扩展式表述 |
| 表 1 不完全信息动态博弈收益表 |
| 表 2 患者首诊决策与医生诊疗策略的博弈支付矩阵 |
根据上述假设,可得患者首诊选择“二级医院”策略的收益为:
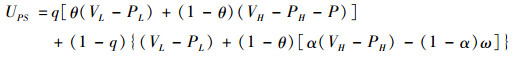
|
(1) |
患者首诊选择“三级医院”策略的收益为:
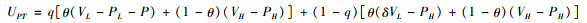
|
(2) |
患者首诊选择“二级医院”策略的复制者动态方程为:
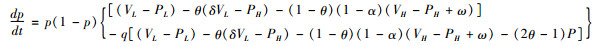
|
(3) |
同理可得医生选择“分级诊疗”策略的收益为:
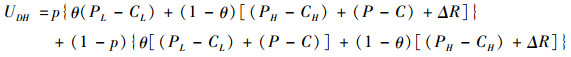
|
(4) |
医生选择“常规诊疗”策略的收益为:
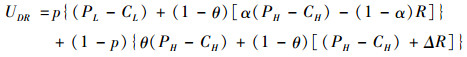
|
(5) |
医生选择“分级诊疗”策略的复制者动态方程为:

|
(6) |
根据Friedman提出的方法,患者和医生演化系统均衡点的稳定性可通过求解并分析该系统的雅可比矩阵的局部稳定解得到。那么上述系统的雅可比矩阵为:
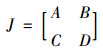
|
(7) |
其中,

|
(8) |
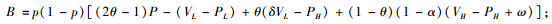
|
(9) |
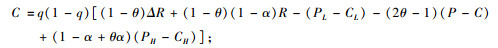
|
(10) |
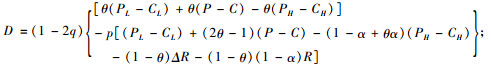
|
(11) |
令该复制者动态系统中式(3)dp/dt=0,式(6)dq/dt=0,得到该雅可比矩阵在5个稳定点处的行列式值和迹见表 3。
| 表 3 均衡点处雅可比矩阵行列式值和迹数值讨论 |
由模型假设可得:
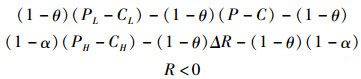
|
(12) |
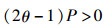
|
(13) |
依据演化博弈中满足detJ>0,trJ < 0的均衡点为系统的演化博弈稳定点,可得(0, 1)和(1, 0)不是系统的均衡点①,对应于策略组合(三级医院,分级诊疗)和(二级医院,常规诊疗)。该结果表明,当患者首诊一致性地选择三级医院时,自利型医生群体的理性决策必不会是分级诊疗;同理,若医生群体诊疗决策均为常规诊疗时,患者群体在自身效用最大化驱使下,定不会首诊二级医院。综上所述,患者就医与医生诊疗博弈系统稳定性主要取决于:
① 式(12)表示若患者均选择“二级医院”时,分工理论下的医生“分级诊疗”策略带给的患者收益优于医生“常规诊疗”诊策略下的患者收益:(PL-CL)-(P-C)-(1-α)(PH-CH)-ΔR-(1-α)R=0;依据复杂型多发病(所占比例为θ)和疑难重症(约占1-θ)的定义和假设,易得θ>0.5恒成立,推得式(13)成立
医生“常规诊疗”策略下,患者选择首诊“二级医院”与“三级医院”的收益差值,令该差值为π1,即得:π1=(VL-PL)-θ(δVL-PH)-(1-θ)(1-α)(VH-PH+ω);患者首诊“三级医院”策略下,医生选择“分级诊疗”与“常规诊疗”的收益差值,令该差值为π2,即得:π2=θ(PL-CL)+θ(P-C)-θ(PH-CH)。以下对不同取值情况下患者就医与医生诊疗博弈的系统稳定性进行分析(表 4)。
| 表 4 患者就医与医生诊疗博弈系统稳定性分析 |
由表 4可得,若医生一致性地选择“常规诊疗”策略,患者选择首诊“三级医院”所得的收益大于选择“二级医院”收益,患者自利性选择“三级医院”;继而若患者均选择首诊“三级医院”时,医生选择“常规诊疗”策略的收益高于其选择“分级诊疗”策略的收益,那么该系统有两个演化均衡点,分别为(三级医院,常规诊疗)与(二级医院,分级诊疗)。其他情形下系统只有(二级医院,分级诊疗)一个演化均衡点,这与中国现阶段医疗改革实践的实际情况相符合。我们将引入数值算例,分析促使患者就医与医生诊疗博弈均衡从(三级医院,常规诊疗)向(二级医院,分级诊疗)转变的各参数的变化及其实际意义。
4 仿真分析参数赋值如下:
取θ=0.6;α=0.8;δ=1.2;ω=300;ΔR=5;R=20;VL=100;PL=30;CL=22;VH=200;PH=50;CH=30;P=20;C=20。得到患者就医与医生诊疗博弈支付矩阵(表 5)。
| 表 5 患者就医与医生诊疗博弈支付矩阵 |
根据上述假设,可得患者首诊选择“二级医院”策略的复制者动态方程为:dp/dt=p(1-p)(12q-8)。
同理,医生选择“分级诊疗”策略的复制者动态方程为:dq/dt=q(1-q)(9.2p-7.2)。
由此得到上述系统雅可比矩阵为:
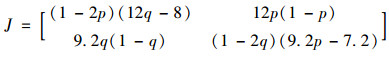
|
系统局部稳定性分析结果见表 6。
| 表 6 局部稳定性分析 |
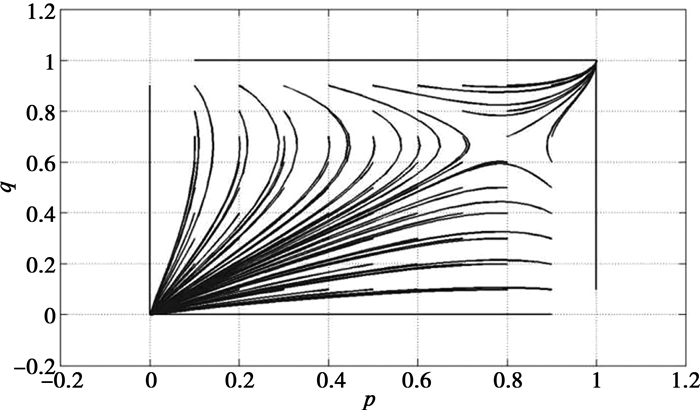
由表 6可得患者首诊决策与医生诊疗策略博弈系统在平面S={(x, y); 0≤x, y≤1}的局部均衡点有5个,分别为O(0, 0),A(1, 0),B(0, 1),C(1, 1)及D(0.78, 0.67)。其演化博弈相位图如图 2所示:其中仅有C(1, 1)和O(0, 0)是系统的演化稳定均衡策略(ESS),分别对应患者首诊二级医院、医生分级诊疗与患者首诊三级医院、医生常规诊疗。
|
图 2 患者首诊就医与医生诊疗博弈相位图 |
图 2鞍点位置表明:在该参数设置下,博弈系统最终会到达稳定均衡点O(0, 0),即患者首诊三级医院,医生采取常规诊疗策略。那么令该情况下的初始值为p=0.3, q=0.3,即假设70%的患者选择首诊三级医院,70%的医生选择常规诊疗策略。下面具体分析调整某些参数变化对该演化系统均衡点的影响。
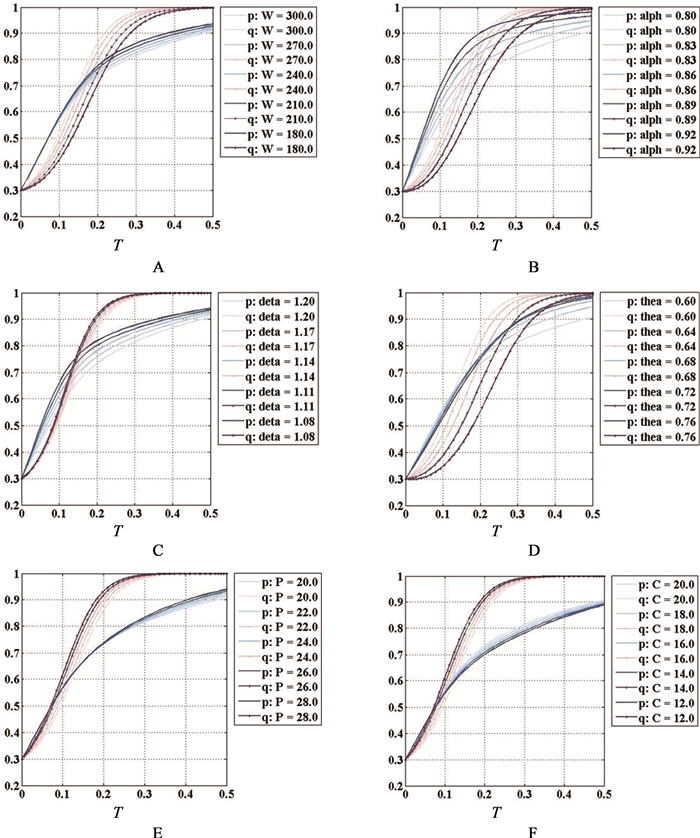
图 3A计算了疑难重症患者仅首诊二级医院的效用损失ω的降低对博弈演化路径的影响。随着时间的推移,初始值由p=0.3;q=0.3逐渐演化为p=0.9363;q=0.9977。且随着仅首诊二级医院所带来的效用损失从300依次降低至180,患者选择首诊二级医院的演化速度逐渐增强(蓝色线型由浅到深变化);医生选择分级诊疗的演化速度逐渐降低(紫色点线型由浅到深变化)。即表明该效用损失的降低会促使患者首诊二级医院的概率的增加,进而引起系统均衡点向(二级医院,分级诊疗)方向演化。
|
图 3 参数变化对患者首诊就医选择和医生诊疗决策博弈演化的影响 |
图 3B计算了疑难重症患者首诊二级医院接受医生常规诊疗继而进入三级医院接受诊疗的概率α的升高对博弈演化路径的影响。随着时间的推移,初始值由p=0.3;q=0.3逐渐演化为p=0.9809;q=0.9923。且随着疑难重症患者首诊二级医院接受医生常规诊疗继而进入三级医院接受诊疗的概率从0.80依次升高至0.92,患者选择首诊二级医院的演化速度逐渐增强(蓝色线型由浅到深变化);医生选择分级诊疗策略的演化速度逐渐降低(紫色点线型由浅到深变化)。即表明该诊疗概率的提高会促使患者首诊二级医院的概率的增加,进而引起系统均衡点向(二级医院,分级诊疗)方向演化。
图 3C计算了复杂型多发病患者A在三级医院与二级医院诊疗的效用比值δ的降低对博弈演化路径的影响。随着时间的推移,初始值由p=0.3;q=0.3逐渐演化为p=0.9416;q=1.0000。且随着复杂型多发病患者A在三级医院与二级医院诊疗的效用比值从1.20依次降低至1.08,患者选择首诊二级医院的演化速度逐渐增强(蓝色线型由浅到深变化);医生选择分级诊疗策略的演化速度也有小幅增强(紫色点线型由浅到深变化)。即表明该效用比值的降低会促使患者首诊二级医院的概率的增加,进而引起系统均衡点向(二级医院,分级诊疗)方向演化。
图 3D计算了复杂型多发病患者A占患者的比例θ的升高对博弈演化路径的影响。随着时间的推移,初始值由p=0.3;q=0.3逐渐演化为p=0.9849;q=0.9930。且随着复杂型多发病患者A占患者的比例从0.60依次升高至0.76,患者选择首诊二级医院的演化速度逐渐增强(蓝色线型由浅到深变化);医生选择分级诊疗策略的演化速度逐渐降低(紫色点线型由浅到深变化)。即表明复杂型多发病患者比例的提升会促使患者首诊二级医院的概率的增加,进而引起系统均衡点向(二级医院,分级诊疗)方向演化。
图 3E计算了患者经由医生分级诊疗需向首诊医院支付的费用P的升高对博弈演化路径的影响。随着时间的推移,初始值由p=0.3;q=0.3逐渐演化为p=0.9394;q=1.0000。且随着经由医生分级诊疗需向首诊医院支付的费用从20.0依次升高至28.0,医生选择分级诊疗策略的演化速度逐渐增强(紫色点线型由浅到深变化);患者选择首诊二级医院的演化速度小幅增强(蓝色线型由浅到深变化)。即表明经由医生分级诊疗需向首诊医院支付的费用的提升会促使医生分级诊疗的概率的增加,进而引起系统均衡点向(二级医院,分级诊疗)方向演化。
图 3F计算了医生分级诊疗下首诊医院需支付的诊断费用C的降低对博弈演化路径的影响。随着时间的推移,初始值由p=0.3;q=0.3逐渐演化为p=0.8896;q=1.0000。且随着医生分级诊疗下首诊医院需支付的诊断费用从20.0依次降低至12.0,医生选择分级诊疗策略的演化速度逐渐增强(紫色点线型由浅到深变化);患者选择首诊二级医院的演化速度逐渐降低(蓝色线型由浅到深变化)。即表明医生分级诊疗下首诊医院需支付的诊断费用的降低会促使医生分级诊疗的概率的增加,进而引起系统均衡点向(二级医院,分级诊疗)方向演化。
5 建议 5.1 促进二三级医院间的分工与合作强化二三级医院功能定位和职能划分,三级医院强化对疑难重症的诊断与治疗的投入、弱化甚至削减大部分二级医院可替代性的常规临床诊断与治疗的投入,二级医院则强化复杂型多发病的临床诊断与治疗,通过典型病例的反复学习与探索,简化流水线式的诊疗流程,节约复杂型多发病患者的诊疗时间,提升二级医院医疗服务的投入产出比;促进二三级医院对点分流中介平台的建立,通过第三方进行二三级医院分级诊疗的对接,提高首诊医院对转诊医院的搜寻效率。
5.2 降低疑难重症患者就诊二级医院的效用损失、提升其就医体验提高二级医院医生的专业素质和业务能力,鼓励二级医院医生到三级医院进行规范化专业技能培训;推进基层医疗卫生机构、二三级医院间的连续性临床诊疗,通过医生互联互通、同质化诊断报告及健康档案的实时云传递,制定以患者为中心,家庭医生、二级医院医生、远程医疗三级医院医生共同参与的连续性治疗方案。
完善二级医院相关基础设施建设,为患者及家属提供舒适的就医环境,提升二级医院的医疗服务质量;优化二级医院患者医疗服务,鼓励二级医院医生提供以基本医疗服务为基准,依据患者个体异质性提供差异化的医疗服务,激励患者主动参与到其诊疗方案的制定与实施,提升患者治疗依从性与改善影响健康的不良生活习惯。
5.3 加强疑难重症患者的疾病预防加强慢性病高危人群的疾病干预,通过辖区内多形式的健康宣教,增强居民对慢性病的重视程度,加之健康档案的有效建立与家庭医生签约制的不断推进,持续地降低因慢性病的不及时干预、不科学治疗管理所引致的疑难重症;持续推进基因检测技术在疑难重症患者基因组中的研究投入,在符合伦理规范要求下结合健康档案对具有家族病史的疑难重症患者进行基因检测,对具有高风险患病率的DNA进行有效识别,并通过生物传感器监测高危人体的DNA、RNA、蛋白质和自身抗体信号,以达到对高危人群的及时干预。
作者声明本文无实际或潜在的利益冲突。
| [1] |
Yip W, Hsiao W. Harnessing the privatisation of China's fragmented health-care delivery[J]. Lancet, 2014, 384(9945): 805-818. DOI:10.1016/S0140-6736(14)61120-X |
| [2] |
陈丽金, 杜纯艳, 黄奕祥. 医疗床位及相关资源供给趋势分析:基于中美对比分析思考我国医疗卫生领域的供给侧改革[J]. 中国卫生经济, 2017, 36(3): 70-73. |
| [3] |
匡莉, 曾益新, 张露文, 等. 家庭医师整合型服务及其医保支付制度:台湾地区的经验与启示[J]. 中国卫生政策研究, 2015, 8(7): 26-35. |
| [4] |
郭有德, 梁鸿. 我国实现分级有序医疗的障碍及对策[J]. 中国卫生政策研究, 2014, 7(6): 6-9. |
| [5] |
王玮玉, 蒋艳, 满晓玮, 等. 基于资本形成账户的北京市医疗卫生功能疏解分析[J]. 中国卫生政策研究, 2017, 10(1): 21-26. |
| [6] |
熊雪晨, 周奕男, 白鸽, 等. 区域卫生规划中病人跨区域流动分析方法及实证研究—以上海市为例[J]. 中国卫生政策研究, 2016, 9(3): 64-68. |
| [7] |
王书平, 薛杰, 孟庆跃. 合理患者流向带来的经济效益分析与影响[J]. 中国卫生经济, 2016, 35(12): 31-34. |
| [8] |
吴凌放, 薄涛, 房良, 等. 以功能协同为导向的卫生服务体系研究:以青岛为例[J]. 中国卫生经济, 2016, 35(11): 45-48. |
| [9] |
Song J, Wen J. A non-cooperative game with incomplete information to improve patient hospital choice[J]. International Journal of Production Research, 2015, 53(24): 7360-7375. DOI:10.1080/00207543.2015.1077284 |
| [10] |
Qiu Y, Song J, Liu Z. A simulation optimisation on the hierarchical health care delivery system patient flow based on multi-fidelity models[J]. International Journal of Production Research, 2016, 1-16. |
| [11] |
向前, 王前, 邹俐爱. 基于利益相关者理论和博弈论的公立医院利益补偿分析[J]. 中国卫生经济, 2012, 31(8): 5-6. |
| [12] |
李习平. 公立医院利益相关者演化博弈均衡研究[J]. 中国卫生经济, 2015, 34(2): 86-89. |
| [13] |
甘筱青, 尤铭祥, 胡凯. 医保报销比例差距、患者行为选择与医疗费用的关系研究—基于三阶段动态博弈模型的分析[J]. 系统工程理论与实践, 2014, 34(11): 2974-2983. |
| [14] |
汪祥松, 杜荣, 艾时钟, 等. 远程医疗背景下社区医院和患者行为选择的演化分析[J]. 工业工程与管理, 2015, 20(2): 130-137. |
| [15] |
艾时钟, 范晓妞. 医院和患者对医疗APP选择行为的演化博弈分析[J]. 中国管理科学, 2015(s1): 34-40. |
| [16] |
张慧林, 成昌慧, 马效恩. 分级诊疗制度的现状分析及对策思考[J]. 中国医院管理, 2015, 35(11): 8-9. |
(编辑 薛 云)