医疗技术和社会保障水平的提高是我国人民对美好生活需要的重要组成部分。经过几十年的努力,我国已经建成了世界上覆盖人数最多(13.64亿人)、覆盖比例最高(96.8%)的基本医疗保险体系[1],但医保支出规模增长过快,居民医疗负担加重的问题也随即凸显。2019—2021年,医保基金总支出从19 945亿元增长到24 011亿元,增长率超过20%;除2020年受疫情影响之外,其他年份的居民人均医疗保健支出增长率均超过了人均可支配收入的增长率。[2]随着医药卫生体制改革的不断深入,医保支付制度作为关系民生的重要部分,其改革也迫在眉睫。2016年国务院印发的《“健康中国2030”规划纲要》明确提出“全面推进医保支付方式改革,积极推进按病种付费、按人头付费,积极探索按疾病诊断相关分组付费、按服务绩效付费,形成总额预算管理下的复合式付费方式”;2020年《中共中央国务院关于深化医疗保障制度改革的意见》要求深化医保支付方式改革,提高医疗保障基金使用效率。
按病种分值付费模式(Diagnosis-intervention Packet,DIP)是基于医院大数据建立的一套完整的医保支付管理系统,在总额预算机制下,根据年度医保支付总额、医保支付比例及各医疗机构病例的总分值计算点值,可应用于医保支付、基金监管、医院管理等多个领域。医保部门基于病种分值和点值形成支付标准,对医疗机构每一病例实现标准化支付,不再以医疗服务项目费用支付,目的是控制医疗机构费用的过快增长和更加有效地利用医疗资源。[3]经过前期多个试点城市的经验积累,2020年11月4日《国家医疗保障局办公室关于印发区域点数法总额预算和按病种分值付费试点城市名单的通知》指出,共有27个省(直辖市)71个城市进入试点名单。
虽然DIP试点已在我国多个城市推广实施,但目前国内研究DIP的文献并不多,大多数是对该政策在不同地区实施的比较或是和其他医保支付方式的比较[4-5]、DIP对公立医院内部管理的影响及建议[6-8]、实施DIP对医生行为的影响[9]及实施DIP的SWOT分析[10, 11]等。而对DIP实施效果的研究大多是通过对某一地区医保数据进行比较,并做简单的分析[12-13],或是利用医院内部的微观数据,对实施DIP前后患者的住院日、住院费用等指标进行比较[14-15]。本文首次使用宏观层面的统计年鉴构建面板数据来研究DIP的政策效应,采用2014年广东省清远市DIP试点作为准自然实验,利用空间计量中的合成控制法构建反事实对照组,探究实施DIP对平均住院日和平均住院费用的影响,使实证结果更具有普适性和借鉴意义,为推进“健康中国”战略、深化医保制度改革及推进DIP支付方式的全覆盖提供实证证明及参考。
1 研究设计 1.1 研究方法 1.1.1 合成控制法广东省清远市于2014年开始试点DIP,省内(除中山市、汕头市)其余城市均在2018年后开始试点,因此,可将实施DIP作为一项准自然实验。根据鲁宾反事实框架理论,试点城市可作为“处理组”,其他备选地区可以作为“对照组”,通过比较处理组和对照组所研究变量的差异,便可得出实施DIP的政策效应。[16]在政策评估中最常用的方法是双重差分法(DID),但使用双重差分法做政策评估的一个重要前提是处理组与对照组在政策实施前具有可比性。在试点地区确定的情况下,非试点地区“对照组”的选择就有一定的主观性和随意性[17],很难找到一个在经济发展状况、医疗卫生水平和人口结构都与清远市相近的,并且没有实施DIP的城市作为对照组,即对照组不一定能够满足平行趋势假设。此外,在试点期间的政策效应还可能受到其他政策影响,因此,较难得到实施DIP的净效应。
合成控制法(Synthetic Control Method)较好地解决了选取对照组的问题,通过将非试点地区进行线性组合,根据对面板数据的处理来确定线性组合的最优权重,人为地构造一个效果良好的对照组。相比于双重差分法,合成控制法的优势在于解决了研究者自己选择对照组的主观性,也减少了内生性问题。Abadie和Gardeazabal提出该方法后[18],越来越多研究者利用其评估政策的实施效应[16-17, 19-21]。因此,本文选用合成控制法对清远市实施DIP的政策效果进行评估。基本思路如下:直接寻找一个与清远完全相似的城市极其困难,可以将没有实施DIP的其他城市通过数学模型拟合出一个与政策实施前的清远在经济、人口、医疗等各方面相似程度较高的“合成清远”,而在政策实施后“真实清远”与“合成清远”的差异即为实施DIP的净效应。实证方法的具体内容阐述如下:
假设可以观测到J+1个地区患者的平均住院日和平均住院费用,第一个地区在T0时期实施了DIP,其余J个未受政策影响的地区则为对照组。用QitN表示第i个地区在t时刻没有实施DIP时患者的平均住院日/平均住院费用,QitI表示第i个地区在t时刻实施DIP时患者的平均住院日/平均住院费用。根据Abadie和Gardeazabal提出的理论框架,模型设置如下:
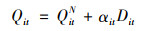
|
(1) |
Dit表示是否为试点地区的虚拟变量,如果地区i在t时刻开始政策试点,则Dit=1,否则Dit=0;而αit则是实施DIP的效果,本文的目标即估计当t>T0时αit的值。对于不受政策影响的地区,则Qit=QitN,对于试点地区来说,t>T0时αit=QitI-QitN=Qit-QitN,其中Qit可以观测得到,而QitN则需要估计,因此,通过构建“反事实”变量来表示QitN。QitN可通过模型表示为
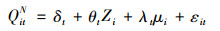
|
(2) |
(2) 式为患者平均住院日/平均住院费用的决定方程,其中Zi是不受政策影响的控制变量,δt是时间趋势,λt是一个(1×F)维观测不到的共同因子,μi是(1×F)维观测不到的地区固定效应误差,εit是每个地区观测不到的暂时影响,均值为0。因此,我们需要求出一个(J+1)维的权重向量W*=(w2*, w3*…wJ+1*),满足对任意的J,WJ≥0,并且w2+…+wJ+1=1。
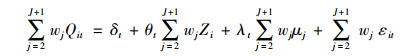
|
假设存在一个向量组W*=(w2*, w3*…wJ+1*)′满足公式(3)、(4):

|
(3) |
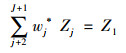
|
(4) |
如果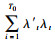
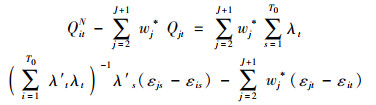
|
(5) |
Abadie等证明在t>T0时,等式(5)右边趋近于0。所以当T0 < t≤T时,可以用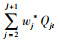
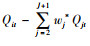
稳健性检验主要包括两种检验方法:安慰剂检验和迭代剔除法。
Abadie认为合成控制法属于比较案例研究的一种,由于合成权重为正的地区数量并不多,故采用大样本理论进行统计推断并不严谨,因此提出了“安慰剂检验”[22],这类似于统计学中的“排列检验”,并适用于任何样本容量。“安慰剂检验”的基本思路是: 依次将所有的对照组全部假想成为处理组,分别合成每一个非试点地区的反事实状态,如果在政策实施后每一个地区与合成地区的政策效应均小于真实试点地区的政策效应,则认为政策冲击效应是存在的。本文假设其余城市同样在2014年开始实施DIP,并将清远作为未实施该政策的城市,然后使用合成控制法依次获得19个城市的反事实状态,如果清远的真实效应与其他城市随机产生的效应差异足够大,则说明清远实施DIP对于减少平均住院日和降低平均住院费用增速的效果是显著的。
迭代剔除法可以检验过度依赖单一权重地区的合成清远与真实清远之间差值的影响,从而检验模型的稳健性。本文利用迭代法对合成清远的拟合结果稳定性进行测验,每次迭代删除一个合成清远权重为正的城市,用来检验合成清远的平均住院日和平均住院费用是否会受到合成城市里各地区权重的影响,删除各权重城市是否会影响最终合成的结果。若结果与原合成结果相同,即有一致的政策效果,说明权重因素不会影响最终的合成结果,政策效应是稳健的。
1.2 数据来源及模型构建合成控制法需要使用试点地区和非试点地区的平衡面板数据进行研究。清远市于2014年开始试点DIP,是广东省第二个试点地区(中山市于2010年开始试点,删除中山市相关数据),故本文选取清远市作为评估对象。本省内部的医保政策有一定的统一性,2018年起广东开始在全省推行DIP,故本文使用2008—2017年广东省各地级市层面的数据进行研究,数据来源于《中国统计年鉴》《中国卫生统计年鉴》《广东卫生健康统计年鉴》及广东省各市的《城市统计年鉴》。因部分统计年鉴无法查阅到相关年份数据,导致数据项“平均住院费用”缺失,最终只录得2011—2017年数据。由于“平均住院费用”为结果变量,可将解释变量时间与之匹配构建面板数据进行评估。最终本文录得广东(除中山市)共20个城市的平衡面板数据。
在模型构建上,合成控制法中选择的解释变量要对结果变量有较强的预测能力,但并不是简单的要求结果变量与解释变量之间存在直接的因果关系。目前,在医疗卫生领域构建的指标体系主要有社会及人口因素、经济因素、医疗卫生因素等,本文选取了可能对DIP实施效果产生影响的部分指标[21],详见表 1。其中,入院强度为本文设置的变量,取年住院人次与总人口的比值,平衡了各市人口总量的差别,用来衡量该地区的住院比例;人均GDP与城镇人均可支配收入对平均住院费用有较大的影响;卫生机构数量、万人医生数量和病床使用率等医疗资源对平均住院日预测能力较好。
| 表 1 模型构建的指标体系 |
表 2展示了利用其他控制组城市构造合成清远的权重系数组合,共有4个地区权重系数大于零,其中河源、江门在合成组中权重较大。为了检验合成清远的拟合效果是否理想,表 3展示了实施DIP之前真实清远与合成清远的各解释变量值,对比发现真实清远与合成清远在主要解释变量上差异度较小,这说明合成清远较好地刻画了真实清远平均住院日的变化情况,从而可以利用合成清远和真实清远的差异来评估政策效应。
| 表 2 合成清远平均住院日的地区权重 |
| 表 3 真实清远与合成清远平均住院日的解释变量对比 |
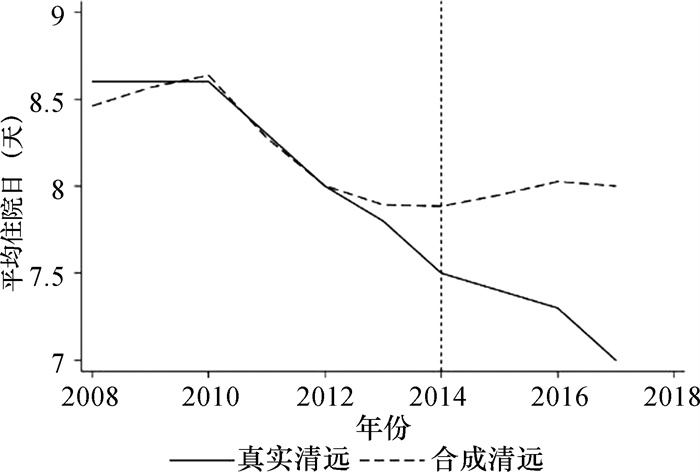
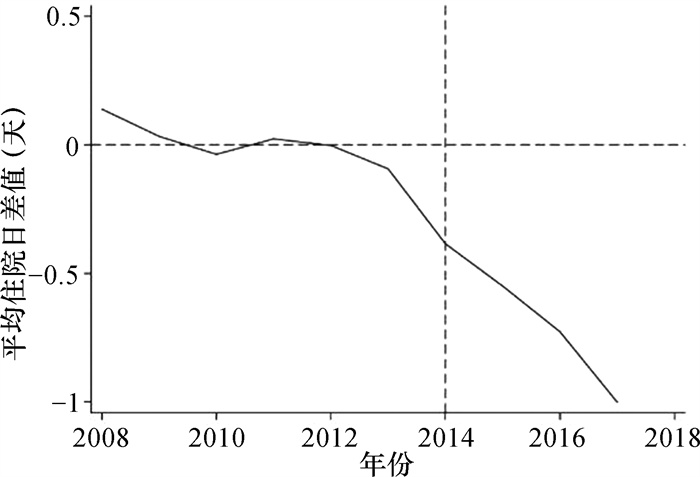
图 1是真实清远和合成清远2008—2017年平均住院日的变化情况,竖虚线位置为DIP试点开始实施的2014年。虚线左侧显示政策实施前真实清远与合成清远平均住院日走势相同;虚线处为实施DIP的第一年,在虚线右侧,真实清远和合成清远在平均住院日上发生了趋势的偏离,真实清远平均住院日逐年下降,合成清远甚至出现上升趋势,这一偏离差异代表了DIP的实施效果。图 2可以看出,真实清远与合成清远平均住院日的差异随时间变化的趋势,真实清远在2013年平均住院日比合成清远少0.1天,而到2017年则扩大到1天,这说明实施DIP有利于减少患者的平均住院日。
|
图 1 2008—2017年真实清远与合成清远平均住院日的变化情况 |
|
图 2 2008—2017年真实清远与合成清远平均住院日差值情况 |
表 4展示了合成清远平均住院费用的各市权重系数组合,同样有4个地区权重系数为正,其中河源、云浮合成的权重最高,分别为0.391和0.327,对合成清远的贡献较大。表 5是真实清远和合成清远在实施DIP前主要解释变量的对比情况,可以发现真实清远和合成清远在主要解释变量上差异很小,合成清远可以很好地刻画变化趋势,合成控制法的拟合效果较为理想。
| 表 4 合成清远平均住院费用的地区权重 |
| 表 5 真实清远与合成清远平均住院费用的解释变量对比 |
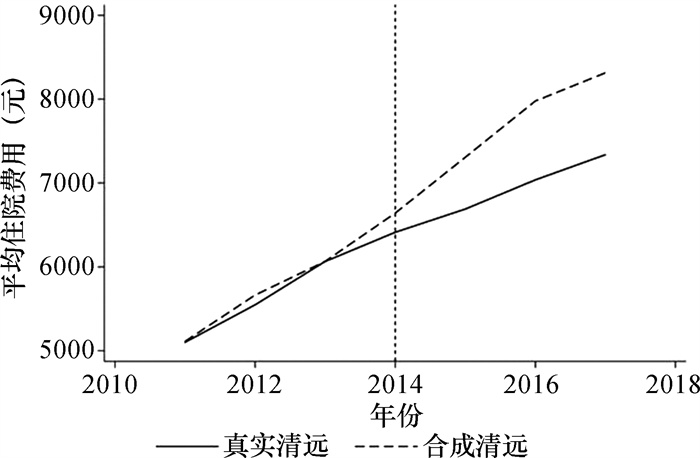
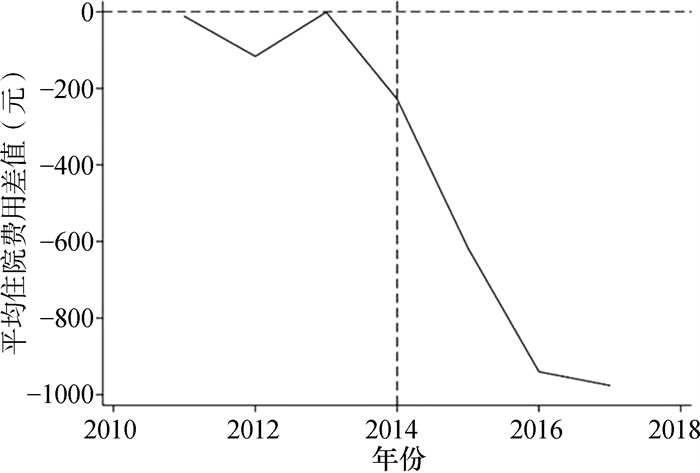
图 3显示了真实清远和合成清远2011—2017年平均住院费用的变化情况。竖虚线为政策实施的2014年,虚线左侧真实清远与合成清远的平均住院费用高度相似;并且试点政策在实施的当年就有明显的效果,2014年合成清远的平均住院费用已显著高于真实清远,在虚线右侧,真实清远和合成清远的偏离程度逐渐扩大,说明真实清远平均住院费用的增速小于合成清远。图 4展示了真实清远与合成清远平均住院费用的差值随时间变化的情况,政策实施前(2011—2013年)两者的差值极小,2014年政策试点后差值明显拉大,且政策实施效果随着时间的推移有逐步扩大的趋势,2017年两者差值已接近1 000元,合成清远比真实清远的平均住院费用高14%左右,证明DIP对于控制住院费用增长有较好的效果。
|
图 3 2011—2017年真实清远与合成清远平均住院费用的变化情况 |
|
图 4 2011—2017年真实清远与合成清远平均住院费用差值情况 |
本文对除清远外其余19个城市进行了“安慰剂检验”,并得到“安慰剂检验”的分布,再将清远的政策效应与之进行对比。
在其余19个城市在进行安慰剂检验时,在政策实施前部分城市合成控制的拟合效果很差,即均方误差(MSPE)较大,则会使政策实施后的变量波动也很大,导致结果的不可信。在剔除MSPE较大的地区后得到的安慰剂检验结果如图 5、图 6所示。可以看出其他城市作为试验城市的政策效应与清远作为试验城市的政策效应差距明显,证明实施DIP对于减少平均住院日和降低平均住院费用增幅的效果不是由偶然因素引起的。
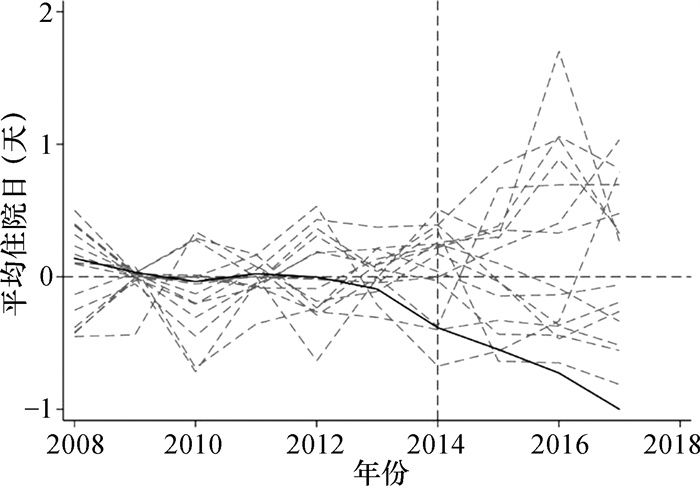
|
图 5 安慰剂检验(平均住院日) |
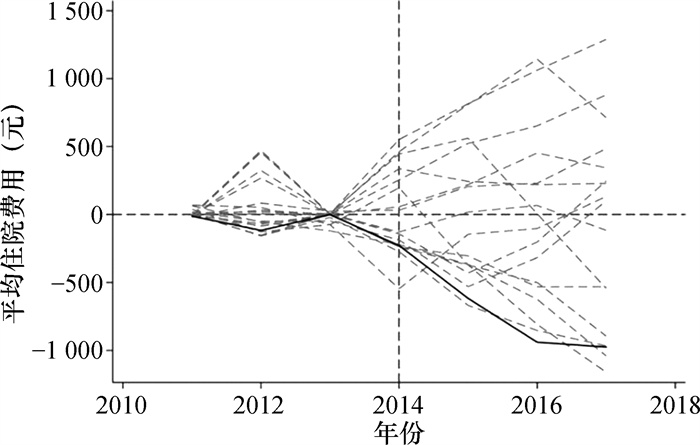
|
图 6 安慰剂检验(平均住院费用) |
其余城市合成反事实清远的权重会对合成的结果产生一定影响,合成清远的权重可能过度依赖某单一用于合成的地区,造成合成清远与真实清远存在一些差别,从而导致政策效应出现偏差,本文通过剔除最大权重地区后再进行合成控制,来证明政策效应的稳健。图 7、图 8展示了剔除最大权重地区后的合成结果,证明实施DIP的政策效应不随合成清远的城市样本变化而改变。
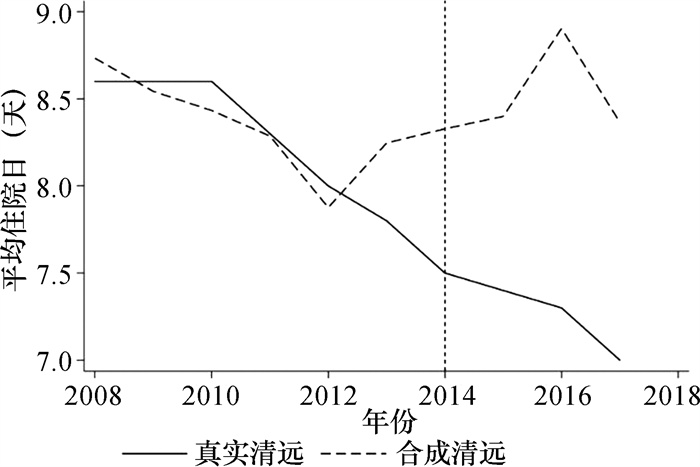
|
图 7 剔除最大权重地区后的平均住院日 |
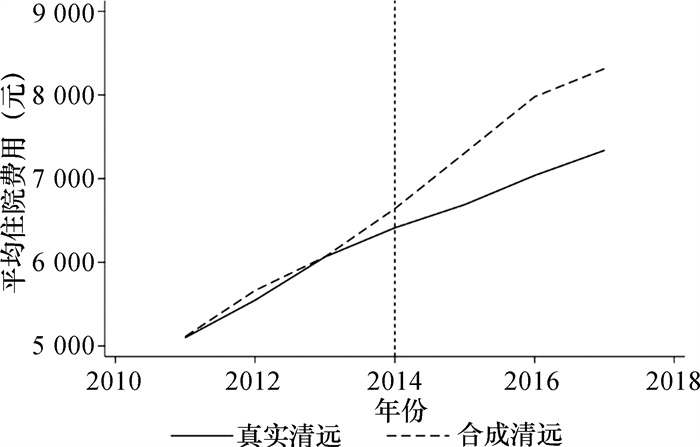
|
图 8 剔除最大权重地区后的平均住院费用 |
本文利用清远市DIP试点作为准自然实验案例,运用合成控制法评估了实施DIP对平均住院日和平均住院费用的影响,实证发现实施DIP可以有效降低患者的平均住院日,提高医院病床的周转率、提升医院的运行效率;降低了平均住院费用的增速,从而减缓了医保基金的支出增速,维护了医保基金的运行安全。清远市医保基金从2012年当年亏空1.5亿元,到2017年整体收支平衡,在实施DIP改革后医保的亏空逐年好转[2],患者也一定程度上减轻了经济负担,住院费用的自付比例降低[23],尤其是药物支出明显下降[24]。在医保基金总额控制下使医院、科室间形成了良性的竞争机制,提高了医院的服务质量[25],医、保、患三方均获得DIP改革的好处。本文的结论为国家推广实施DIP,深化医保支付方式改革提供了一定的理论及实证依据。
DIP作为我国原创、有中国特色的医保支付方式[26],虽然借鉴了国外成熟的按疾病诊断相关分组付费(DRG)的方式,也有前期多个城市的试点经验,但在实际操作中仍存在一些问题需要改进,结合以上对清远市的研究,提出如下建议:
对于各市的医保管理部门,对病种分值的设置、病种覆盖的范围和诊治方式的划分不应照搬原试点城市的政策。应在国家技术规范的指导下利用当地具体的病种特点和医保数据,结合当地医疗资源配置现状,更加科学合理地设置病种分值库,这是按病种分值付费产生良好效果的基础。在不同级别医疗机构的系数及报销比例的设定上,应该与分级诊疗相结合,通过实施按病种分值付费引导患者的就医选择,比如治疗常见病在基层医疗机构的起付线低于三级医院的起付线,而报销比例则基层医疗机构更高,运用此方式推动“基层首诊、双向转诊、急慢分治、上下联动”。[27]还需建立与医院的沟通机制,及时调整医院在实施中发现的不合理制度设定,纠正实施中的问题,逐步完善当地医保支付政策。医保部门也应针对DIP实施过程中医院充点数、组别高套、降低住院质量等不良行为进行监督,利用大数据监测来保证医疗服务质量;并发挥其考核主体的作用,建立激励机制,使DIP真正让多方收益。
对于医院来说,前期应建立高质量的病案、病例管理制度,为推进病种成本核算和分值设定提供依据,也借此提升医生对于病案的重视程度,推进病案管理的标准化;并更新组织架构,完善信息化系统,以满足科室协作、医疗质量评估、绩效考核等方面需求;提升医院的管理水平,做好成本预算,加强成本控制,杜绝小病大治、过度用药等不良行为;院内还需加强政策的宣传培训,使医护人员了解DIP的内容,落实到临床环节,规范医疗行为。
需要说明的是,2018年广东全省开始逐步推行DIP,受制于数据问题,本文仅研究了试点城市2014—2017年的短期政策效应,且前期拟合数据年份不够长。2021年,全国71个城市开始试点DIP,相信之后会获得更多的试点数据,政策效应进一步显现,并能提出更加有针对性的建议。
作者声明本文无实际或潜在的利益冲突。
| [1] |
国家卫生健康委统计信息中心. 2018年全国第六次卫生服务统计调查报告[M]. 北京: 人民卫生出版社, 2021.
|
| [2] |
韦薇. 广东省基本医疗保险按病种分值付费政策研究[D]. 广州: 暨南大学, 2020.
|
| [3] |
国家医疗保障按病种分值付费(DIP)技术规范[Z]. 2020.
|
| [4] |
李秋莎, 杨春晓, 赵兹旋, 等. 我国按病种分值付费(DIP)政策研究——基于国家、省、市三级的比较分析[J]. 中国卫生政策研究, 2022, 15(7): 8-15. |
| [5] |
傅卫, 江芹, 于丽华, 等. DRG与DIP比较及对医疗机构的影响分析[J]. 中国卫生经济, 2020, 39(12): 13-16. |
| [6] |
李烨楠, 吴丹枫. 基于大数据按病种分值付费的公立医院成本管理[J]. 中国卫生资源, 2022, 25(3): 315-317. |
| [7] |
陈继芳, 白丽萍, 谭卉妍, 等. 广东省按病种分值付费实践及对医院医保管理的启示[J]. 中国医院管理, 2022, 42(3): 63-66. |
| [8] |
杨雅棋, 齐新红, 韩笑, 等. 按病种分值付费下公立医院全面预算管理与成本核算探讨[J]. 中国医院, 2021, 25(11): 5-7. |
| [9] |
谭清立, 刘思妍, 柳丹玲, 等. 按病种分值付费对医生行为的影响——基于实验经济学[J]. 中国卫生政策研究, 2021, 14(9): 14-19. |
| [10] |
束嘉俊, 黄晖, 陈怡, 等. 基于医保患三方视角的按病种分值付费SWOT分析[J]. 卫生经济研究, 2022, 39(1): 36-39. |
| [11] |
景秀雯, 王健, 梁坤, 等. 实行总额控制下按病种分值付费的SWOT分析[J]. 中国当代医药, 2019, 26(30): 150-153. |
| [12] |
刘雨阳, 陈贵梅, 徐王权, 等. 芜湖市区域总额预算下按病种分值付费效果评价[J]. 医学与社会, 2022, 35(8): 100-104. |
| [13] |
张仲芳. 总额控制下的医疗保险"按病种分值付费"改革研究——基于南昌市城镇职工医保的实践[J]. 社会科学家, 2016(12): 47-51. |
| [14] |
蔡杰. 按病种分值付费实施效果的实证研究[J]. 中国病案, 2021, 22(4): 28-30. |
| [15] |
詹林城, 苏华冠, 卢智略, 等. 按病种分值付费控制住院费用及住院日的效果分析[J]. 中国医院统计, 2020, 27(1): 88-90. |
| [16] |
王超群, 杨攀续. 两险合并实施对生育保险覆盖面的影响——基于合肥市的合成控制研究[J]. 华中科技大学学报(社会科学版), 2021, 35(6): 44-55. |
| [17] |
于新亮, 刘慧敏, 杨文生. 长期护理保险对医疗费用的影响——基于青岛模式的合成控制研究[J]. 保险研究, 2019(2): 114-127. |
| [18] |
Abadie A, Gardeazabal J. The Economic Costs of Conflict: A Case Study of the Basque Country[R]. The American Economic Review, 2003.
|
| [19] |
杨耀宇, 付梦媛. 分级诊疗的制度效果评估[J]. 统计与决策, 2019, 35(23): 105-108. |
| [20] |
唐文熙, 张梦然, 丁文裴, 等. 合成控制模型在卫生政策评估中的应用[J]. 中国卫生经济, 2020, 39(4): 15-18. |
| [21] |
Zang X, Zhang M, Wei S, et al. Impact of public hospital pricing reform on medical expenditure structure in Jiangsu, China: a synthetic control analysis[J]. BMC Health Services Research, 2019, 19(1). |
| [22] |
Abadie A, Diamond A, Hainmueller J. Synthetic Control Methods for Comparative Case Studies: Estimating the Effect of California's Tobacco Control Program[J]. Journal of the American Statistical Association, 2010, 105(490): 493-505. |
| [23] |
陈曼莉, 赵斌. 实行按病种分值付费制度的实践经验及启示[J]. 中国卫生经济, 2017, 36(6): 38-41. |
| [24] |
Lai Y, Fu H, Li L, et al. Hospital response to a case-based payment scheme under regional global budget: The case of Guangzhou in China[J]. Social Science & Medicine, 2022, 292: 114601. |
| [25] |
Qian M, Zhang X, Chen Y, et al. The pilot of a new patient classification-based payment system in China: The impact on costs, length of stay and quality[J]. Social Science & Medicine, 2021, 289: 114415. |
| [26] |
黄毅, 朱怡. 广东经验对按病种分值付费国家试点城市的启示和思考[J]. 华西医学, 2021, 36(12): 1739-1743. |
| [27] |
王奕婷, 王坚强, 莫显昆. 长沙市城乡居民基本医疗保险病种分值付费改革对分级诊疗的影响[J]. 经济地理, 2021, 41(12): 94-99. |
(编辑 薛云)





