2. 江苏省健康研究院 江苏南京 211112;
3. 南开大学金融学院 天津 300350
2. Jiangsu Provincial Institute of Health, Nanjing Jiangsu 211112, China;
3. School of Finance, Nankai University, Tianjin 300350, China
我国专利药品价格经历了“向定价部门申请‘单独定价’”到“政府指导定价”再到“公开透明,多方参与的谈判机制形成价格”的转变。近年来,我国为进一步提高患者用药的可负担性与可及性,采取了医保价格谈判、“零关税”等一系列降低专利药品价格的措施。其中,对专利药品进行价格谈判,并将其纳入医保目录的工作逐渐展开并取得一定成果。根据2016—2022年谈判结果可知,随着谈判工作的不断推进,谈判成功的药品数量不断增多,谈判成功率先升后降,自2016年的60%上升至2018年的94.4%后,逐渐稳定至2021—2022年的80%左右,谈判成功药品价格的平均降幅则始终稳定在60%左右。然而,相较于常用专利药品,目前通过谈判的药物比例偏低,推进专利药品价格谈判仍为今后我国医疗卫生保障的重点工作之一。
目前,国内对于医保价格谈判的研究主要停留在价格谈判机制框架构建和国外相关经验总结两方面,前者强调谈判体制建设和第三方监管[1-2];后者发现价格谈判的制度设计需要将参与谈判主体的行为需求与临床需求相结合,既通过合理的制度设计使专利药品价格有效降低(以美国为代表),也充分考虑医保基金和患者经济的承受能力,同时更需兼顾医药企业经济效益,使其保持研发动力(以澳大利亚为代表)。[3-4]根据各国的谈判经验可知,对于由政府提供基础医疗保障的国家,谈判主体为医保部门与厂商,谈判基本围绕药物经济学或卫生技术评估结果所显示的药品价值展开。[5]从政府角度而言,专利药的成本效益、临床效用和医保基金预算等因素为影响药品价格谈判的关键所在[6];而对于医药制造商而言,更多的需要考虑专利药研发的实际成本和沉没成本、营销渠道、销量以及支付方式。[7]因此,政府机构与厂商进行谈判博弈将基于上述行为目标展开。
综上,鉴于我国药品价格谈判起步较晚,目前我国实施的“公开透明、多方参与”的谈判体系尚不成熟,亟需对谈判关键环节、谈判主体、谈判依据进行深入剖析。演化博弈是在博弈框架的基础上,通过参与者不断学习调整达到均衡结果,逐渐趋于某个演化稳定策略,已广泛应用于价格谈判的研究中[8]。专利药价格谈判实际操作过程中恰恰也是一个循环往复的过程,可将其视为复制动态模型,适用于演化博弈理论。因此,本文立足于现有谈判结果,对我国专利药品医保价格谈判进行演化博弈分析,探索价格谈判的稳定状态及影响因素的作用路径。
2 我国专利药品价格谈判的演化博弈模型构建 2.1 我国药品价格谈判的演化博弈框架 2.1.1 博弈模型的基本假设及要素我国专利药价格谈判主体为政府机构和医药企业,结合演化博弈理论基础,建立以下假设:第一,有限理性,即双方在进行专利药价格博弈谈判的过程中,受到我国药品定价、医疗保险以及招标采购等政策体系的影响,并尊重市场规律。博弈双方均在此前提下,追求自身利益最大化,双方均具有中止谈判的动机及权力。第二,非完全知识假定,即博弈的局中人对于博弈相关知识的获取、分析和判断能力有限,无法做到完备无误。第三,策略惯性假设,参与博弈的两个群体——政府机构与医药企业均在信息不对称、有限理性的前提下,具有一定的经验学习规律和行为逻辑。第四,政府机构与医药企业进行非合作博弈。第五,本文仅分析单家医药企业仅有一种专利药品参与谈判,暂不考虑多个药品的联动情况。
基于上述假设,本文博弈模型的要素有以下几点:
第一,博弈的局中人:政府机构、医药企业。
第二,局中人的行动策略:(1)企业的行动策略集合A={a1,a2}:企业降低专利药价格而进入医保目录以期望销量上升,即a1=同意降价,a2=拒绝降价。(2)政府机构的行动策略集合为B={b1,b2}:政府机构与企业通过谈判协商降低专利药物价格,并承诺将其纳入医保目录,即b1=纳入目录,b2=拒绝纳入目录。
第三,支付函数:(1)当企业与政府机构达成专利药价格谈判一致时,专利药价格为P2,同时预计销量为N2;与之对应的,当专利药未经过价格谈判时,其价格与销量分别为P与N。(2)政府机构在未经过谈判将专利药纳入到医保目录时,其收益(包括政府支出和社会声望等)为G;而当专利药经过价格谈判并纳入到医保目录后,政府机构获得的社会声望(患者健康效益等)以Rg衡量,则其总收益为G-N2P2+Rg;当专利药生产企业基于自身利益,拒绝降价,遭受一定的声誉损失Rp。(3)企业同意和拒绝降价的概率分别为x和1-x(0≤x≤1);政府机构将专利药纳入和拒绝纳入医保目录的概率分别为y和1-y(0≤y≤1)。
2.1.2 博弈支付矩阵构建及分析根据上述假设,结合企业与政府机构进行价格谈判过程中各自的行为需求,建立如表 1所示的价格谈判博弈模型。
| 表 1 政府机构与医药企业参与的专利药价格博弈支付利益矩阵 |
当医药企业同意降价时,根据政府是否同意将专利药纳入医保目录而决定二者是否获得社会收益,仅当二者均同意将专利药纳入医保目录时,二者才能同时获得社会声誉。此时,政府机构面临两种选择:第一,选择付出N2P2的医保基金对专利药进行报销,以获得社会声誉与人民的健康效益,此时二者收益为(N2P2+Rp,G-N2P2+Rg);第二,认为谈判价格不理想,宁愿付出Rg也不批准该药物进入医保目录并报销,二者收益分别为(N2P2,G-Rg)。当医药企业拒绝降价时,政府机构同样面临两种选择:第一,接受对谈判药物进行报销,此时即使谈判不成功,政府机构也不会有声誉损失,二者收益分别为(NP-Rp,G-N2P2);第二,拒绝将专利药纳入医保目录,二者均保持未展开谈判的原始收益(NP,G)。
2.2 专利药医保价格谈判演化博弈模型的稳定性分析 2.2.1 演化博弈模型的适应度分析根据表 1中的支付矩阵可得,企业同意降价与拒绝降价的适应度分别为:
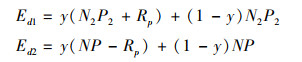
|
则医药企业的平均适应度为:
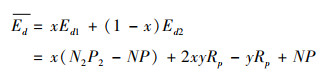
|
同理,政府机构将专利药纳入和拒绝纳入医保目录及总体平均适应度分别为:
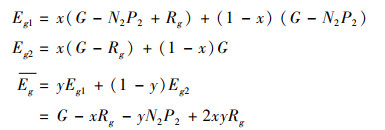
|
根据上述我国现实背景及上述模型建立的有限理性、信息不对称等假设条件下,专利药价格谈判博弈是一个复制动态模型:政府机构与各个医药企业在谈判过程中的策略选择,均会被参与谈判的其他医药企业或参与次年谈判的主体双方所参考复制,通过双方不断地进行谈判经验学习,最终将达到稳定的策略均衡。
综上,可得出医药企业的复制动态方程:
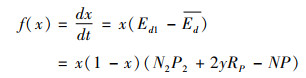
|
同理可得,政府机构的复制动态方程:
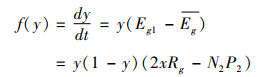
|
分别令f(x)=0,f(y)=0,可解得:
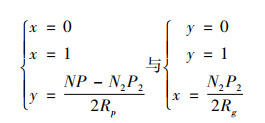
|
因此,该演化博弈模型的平衡点分别为A(0, 0)、B(0, 1)、C(1, 0)、D(1, 1)和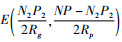
由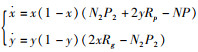

|
根据Liapunov第一法,判断各平衡点的雅克比矩阵特征值是否具有负实部,进而判断该点是否稳定。
该演化博弈模型的雅克比矩阵为:
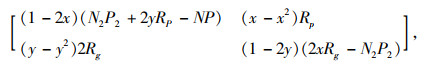
|
得到特征方程[(1-2x)(N2P2+2yRP-NP)-λ][(1-2y)(2xRg-N2P2)-λ]-4RgRP(x-x2)(y-y2)=0。
根据Hurwitz判据,多项式方程λn+a1λn-1+a2λn-2+…an-1λ+an=0所有根具有负实部的充要条件是:
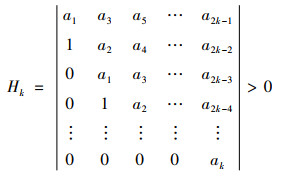
|
分别将平衡点A、B、C、D和E带入,化简得到如表 2所示结果。
| 表 2 药品医保价格谈判演化博弈平衡点Hurwitz判据 |
实际谈判过程中,即使政府机构所获得的社会效益Rg与N2P2大小未能确定,但其理论上大于谈判成功后对该专利药品报销额度的一半,即Rg>0.5N2P2。以下将对变量N2P2、NP、Rg、Rp大小进行讨论,分别判断五个平衡点的稳定性。
(1) 当2Rp+2Rg>NP时,讨论N2P2+Rp与NP的大小关系。当政府与医药企业的社会收益的两倍大于专利药谈判前的销售额时,分N2P2>NP与N2P2 < NP两种情况讨论,当N2P2+Rp < NP时,N2P2大于NP的情况不存在,因此,得到如表 3所示结果。其中,由于专利药经过谈判降价进入医保目录后,其销量将有大幅提升(2016年谈判的三种药品销量均较谈判前上升30%以上),因此,专利药品谈判前后的销售额差距有限,即使当N2P2+Rp < NP时,2N2P2+2Rp也必定大于NP,即0.5NP < N2P2+Rp < NP。
| 表 3 2Rp+2Rg>NP下该药物医保价格谈判演化博弈的局部稳定性结果 |
通过上述分析可知,平衡点A(0, 0)与D(1, 1)在2Rp+2Rg>NP,N2P2+Rp>NP时、A(0, 0)当0.5NP < N2P2+Rp < NP且N2P2 < NP时,为该专利药品演化博弈的稳定点。
(2) 当2Rp+2Rg < NP时,讨论N2P2+Rp与NP的大小关系。同上,当政府与医药企业社会收益的两倍小于专利药谈判前的销售额时,分N2P2+Rp>NP与0.5NP < N2P2+Rp < NP两种情况讨论,得到如表 4所示结果。
| 表 4 2Rp+2Rg < NP下该药物医保价格谈判演化博弈的局部稳定性结果 |
因此,当2Rp+2Rg < NP且N2P2 < NP,仅有点A(0, 0)为稳定点。
综上可知,当2Rp+2Rg>NP、Rg>0.5N2P2且N2P2+Rp>NP、N2P2 < NP时,专利药医保价格谈判演化博弈的相位图如图 1所示。

|
图 1 演化博弈相位图 |
在上述演化博弈理论分析基础上可知,仅有在2Rp+2Rg>NP、Rg>0.5N2P2且N2P2+Rp>NP条件下,存在谈判一致的稳定状态,因此, 分别设立NP>N2P2和N2P2>NP的情况,改变影响专利药品价格谈判博弈过程的参数,并对该演化博弈稳定模型进行情景仿真,分析各参数及初始策略对系统演化路径的影响。
3.1 当NP < N2P2时,初始策略及参数敏感性分析 3.1.1 初始策略对演化稳定状态的影响分析取Rg=3,Rp=2,N2P2=3,NP=2为原始的演化路径,初始策略分别从(0.1, 0.1)、(0.3, 0.3)、(0.5, 0.5)和(0.1, 0.9)、(0.3, 0.7)、(0.5, 0.5)、(0.7, 0.3)、(0.9, 0.1)变化,得到如图 2所示结果。
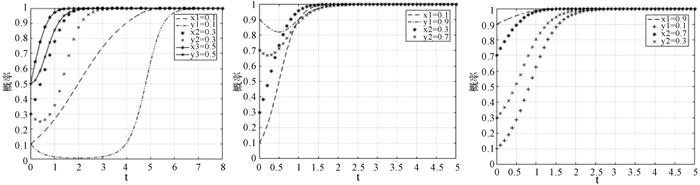
|
图 2 当NP < N2P2时初始策略对演化稳定状态影响 |
如图 2所示的仿真结果显示,当初始策略(x, y)同向和反向变化时,博弈双方达成谈判一致稳定结果的时间随x和y的增加而减少。综合比较图 2的后两个子图发现,相较于局中人决策的初始概率反向变化,同步变化的概率将使达到稳定结果的时间延长,即谈判学习的次数增多。
3.1.2 改变Rg,探究其对演化稳定状态的影响(1) 取Rg=4,Rp=2,N2P2=3,NP=2,初始策略同3.1.1,横向比较三个子图,可发现同图 2一致的规律。除此之外,纵向比较图 2和图 3可知,随着Rg的升高,无论初始策略同向还是异向变化,博弈双方达成谈判一致的稳定结果次数均有所缩短。
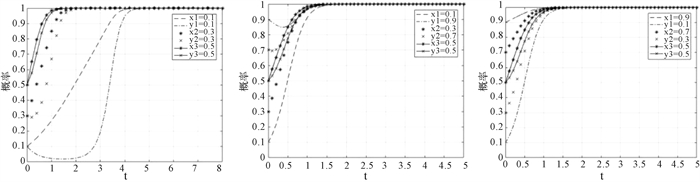
|
图 3 当NP < N2P2且Rg增加时初始策略对演化稳定状态影响 |
(2) 取Rg=2,Rp=2,N2P2=3,NP=2,初始策略变化同3.1.1,除了同样符合图 2所示结论外,验证了Rg与达成谈判稳定结果的学习次数呈负相关关系的规律①。
① 因篇幅所限,此图不做单独展示,感兴趣的读者可与作者联系。
3.1.3 改变Rp,探究其对演化稳定路径的影响。(1) 取Rg=3,Rp=1.5,N2P2=3,NP=2,初始策略变化同3.1.1,得到如图 4所示结果,横向比较三个子图发现图 2所示规律依然成立,纵向比较图 2与图 4发现,Rp的减少使得达成谈判一致的稳定时间略有延长。
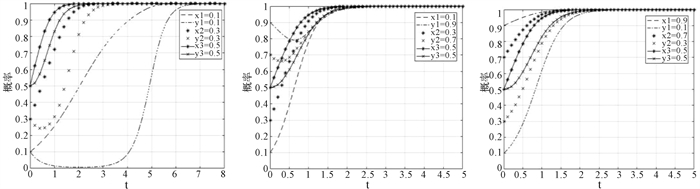
|
图 4 当NP < N2P2且Rp减少时初始策略对演化稳定状态影响 |
(2) 取Rg=3,Rp=2.5,N2P2=3,NP=2,初始策略变化同3.1.1,得到与图 4类似的结果,该结果进一步验证了Rp与达到谈判一致的稳定结果时间成反向变化这一结论1。
3.2 当NP>N2P2时,初始策略及参数敏感性分析 3.2.1 初始策略对演化稳定状态的影响分析取Rg=3,Rp=2,N2P2=2,NP=3为原始的演化路径,初始策略分别从(0.1, 0.1)、(0.27, 0.27)、(0.3, 0.3)、(0.5, 0.5)和(0.1, 0.9)、(0.3, 0.7)、(0.5, 0.5)、(0.7, 0.3)、(0.1, 0.9)变化,得到如图 5所示结果。
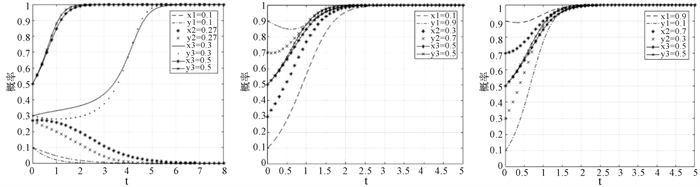
|
图 5 当NP>N2P2时初始策略对演化稳定状态影响 |
由图 5可知,局中人初始策略同步变化时,初始策略影响演化稳定状态:(x, y)均处于(0.27, 0.3)区间内存在阈值,当超过该阈值时,二者演化博弈稳定结果将趋向于谈判一致,并随着(x, y)初始值升高,达到稳定状态时间缩短;当低于该阈值时,二者演化博弈的稳定结果将趋向于谈判破裂,且随着(x, y)初始值越低,达到稳定状态的时间越短。综合比较图 5的后两个子图可知,局中人初始策略的反向变化将使二者均趋向于达成谈判一致的演化稳定状态,且随着x的升高和y的降低,达到演化稳定状态的时间略有缩短。
3.2.2 改变Rg,探究其对演化稳定状态的影响(1) 取Rg=4,Rp=2,N2P2=2,NP=3,初始策略同3.2.1变化,得到如图 6所示结果。横向比较三个子图可知依旧存在图 5所示规律,纵向比较图 5与图 6发现,随着Rg的增加,达到均衡稳定状态的时间逐渐缩短,当初始策略同向变化时,改变演化稳定结果的初始策略阈值从(0.27, 0.3)内降低至0.25。
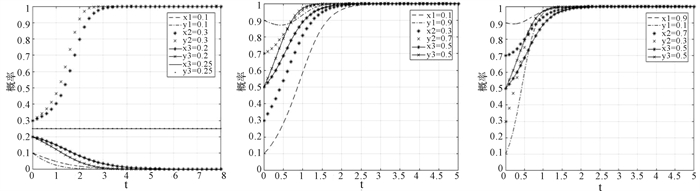
|
图 6 当NP>N2P2且Rg增加时初始策略对演化稳定状态影响 |
(2) 取Rg=2,Rp=2,N2P2=2,NP=3,初始策略同3.2.1变化,依然显示了图 5所示规律。纵向比较之后再次验证:随着Rg的降低,达到稳定状态的时间均延长,且当初始策略同向变化时,导致演化稳定状态分别为谈判一致和谈判破裂的阈值升高至(0.3, 0.5)间①。
① 因篇幅所限,此图不做单独展示,感兴趣的读者可与作者联系。
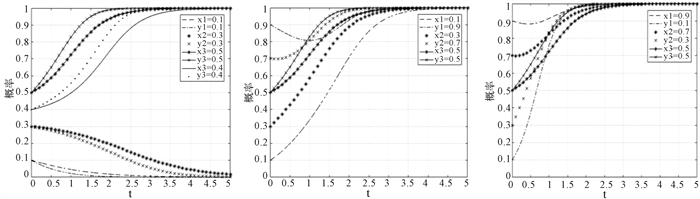
3.2.3 改变Rp,探究其对演化稳定路径的影响(1) 取Rg=3,Rp=1.5,N2P2=2,NP=3,初始策略同3.2.1变化,得到如图 7所示结果。分析三个子图可知图 5所示规律依然成立,纵向比较图 5与图 7可知,随着Rp的减少,当初始策略同向变化时,改变演化稳定结果的初始策略阈值从(0.27, 0.3)内升高至(0.3, 0.4);无论初始策略同向变化或异向变化,达到稳定状态的时间均有所延长。
|
图 7 当NP>N2P2且Rp减少时初始策略对演化稳定状态影响 |
(2) 取Rg=3,Rp=2.5,N2P2=2,NP=3,初始策略同3.2.1变化,图 5所示规律依然成立,随着Rp的增加,达到稳定状态的时间均略有缩短,且当初始策略同向变化时,改变演化稳定结果的初始策略阈值也有所降低。①
① 因篇幅所限,此图不做单独展示,感兴趣的读者可与作者联系。
4 实证检验除了数值模拟之外,为了进一步贴合实际谈判情况,本文选择2016年谈判成功的三个药品:吉非替尼、埃克替尼与富马酸替诺福韦,分析其销售情况与后续谈判意愿。本文数据来自米内网,共收集上述三个药品原研厂商在2013—2021年间于上海市、北京市、南京市、哈尔滨市、天津市、太原市、广州市、成都市、杭州市、武汉市、沈阳市、济南市、深圳市、石家庄市、福州市、西安市、郑州市、重庆市、长春市、长沙市等二十个城市公立医疗机构的销售情况,表 5为描述性统计结果。总体来看,埃克替尼销售额最高,吉非替尼次之,替诺福韦销售额最低。与此同时,不同城市间销售量与销售额也有较大差异。
| 表 5 描述性统计结果 |
本文以2017年对三种药品进行分组,比较专利药品谈判前后三种药品销售额与销售量的组间均值,采用单样本T检验的方法观察谈判前后三种药品销售量与销售额的差异,得到如表 6所示结果。总体来看,2016年通过谈判的三种药品相较于谈判前,在谈判后三者总的销售额与销售量均具有显著且大幅的上涨。具体来看,在销售量方面,三种药品的销售量相较于谈判前,均具有显著的大幅提升,充分说明专利药品经谈判后纳入医保目录,极大程度上促进了其销售量的大幅上升;在销售额方面,尽管吉非替尼的销售额在谈判后也有上升,但结果并不显著,埃克替尼与替诺福韦谈判后的销售额大幅上升,且该结果在1%的置信水平下有统计学意义。在对上述三种药品谈判前后销售量与销售额的增长有了充分的预期之后,2019年谈判药品续约时,三种药品均续约成功,此结果说明企业对于专利药品的预期销售量能够一定程度上影响企业谈判与续约积极性。
| 表 6 谈判前后三种药品的组间差异 |
谈判前后的销售额影响演化稳定结果,当专利药品经过谈判降价后的销售额大于谈判前时,无论双方初始策略如何变化,均能达成谈判一致的演化稳定结果;若经过谈判降价后的销售额低于谈判前,即进入医保目录后带来的销量增加无法弥补降价带来的冲击,谈判演化稳定结果则取决于谈判双方初始策略的取值以及变化方向。因此,在专利药价格谈判过程中,为达到谈判一致的演化稳定结果,政府机构需出台相应的配套措施,确保落实谈判结果落地,使进入医保目录的专利药品销量确有大幅提升——此举不但有利于增加后续参与谈判的专利药品降价成功的概率,更是能够达到惠及更多患者的根本目标。
5.2 初始意愿影响演化稳定结果,谈判前需明确各自谈判目标从仿真模拟结果可知,初始策略的取值及变化方向影响演化稳定结果:其他条件保持不变,当初始策略同向变化时,随着谈判前后的销售额的不同,初始策略的取值将导致达成演化稳定结果的不同;当初始策略异向变化时,演化稳定结果始终为谈判一致,且博弈双方的初始策略越靠近1,达到谈判一致的稳定结果时间越短。该结论说明博弈双方的谈判初始意愿对谈判结果有重要影响——对政府机构而言,应重视谈判初期的药物遴选、药品价值评估等环节,明确谈判目标;对医药企业而言,在谈判降价后销量不确定的情况下,参与谈判前的市场调研工作、社会责任及企业发展前景规划则显得尤为重要,企业自身的经济收益、社会责任及发展定位直接关系谈判结果。
5.3 政府及药企的社会声誉反向影响演化稳定时间,二者应承担惠及国民健康的社会责任政府及医药企业的社会声誉作为影响对谈判演化稳定的因素,对于达到稳定状态的时间有一定影响:无论谈判前后专利药销售额的大小及初始策略如何变化,政府及医药企业社会声誉与博弈双方达成谈判演化稳定的时间均呈负相关关系。该结果从理论上证明,对于政府机构与医药企业而言,除了需要考虑医保基金的可负担性与经济收益外,谈判时二者所承担的社会责任也发挥重要作用。专利药品经谈判降价而进入医保目录,本质上是为了提高国民健康效益,降低患者用药的经济负担。因此,在谈判过程中双方应从社会公益角度出发,各自应承担惠及国民健康的社会责任。
最后,值得注意的是,由于本文设定理论模型时假设每个医药企业仅有单个药品参与谈判,尚未考虑单个医药企业有多个产品同时参与谈判所带来的联动效应,使得本文研究结果具有一定局限性,更多地适用于单个药品谈判情境。
作者声明本文无实际或潜在的利益冲突。
| [1] |
刘颖, 杨健. 国家药品价格谈判的法律规范框架研究[J]. 中国卫生政策研究, 2017, 10(6): 20-24. DOI:10.3969/j.issn.1674-2982.2017.06.004 |
| [2] |
郭莹, 管超超, 张大为. 我国创新药物的价格谈判机制探析[J]. 中国药业, 2015, 24(14): 1-2. |
| [3] |
李金良, 朱海林. 从国际经验视角看我国谈判机制形成药品价格[J]. 中国卫生经济, 2015, 34(12): 94-97. |
| [4] |
伍琳, 陈永法. 澳大利亚专利药价格谈判管理经验及其对我国的启示[J]. 价格理论与实践, 2017(3): 89-92. |
| [5] |
Sussex, Towse, Devlin. Operationalizing Value-Based Pricing of Medicines-A Taxonomy of Approaches[J]. Pharmaco Economics, 2013(31): 1-10. |
| [6] |
Kw on, Godman. Drug Pricing in South Korea[J]. Applied Health Economics and Health Policy, 2017(15): 447-453. |
| [7] |
X ie. Highly Priced Gene Therapies: A Wake-Up Call for Early Price Regulation[J]. Pharmaco Economics, 2018(36): 883-888. |
| [8] |
孙晓华, 胡林, 张国峰. 中外铁矿石价格谈判的演化博弈分析[J]. 南京财经大学学报, 2010(4): 14-18. |
(编辑 刘博)