2. 哈尔滨医科大学卫生管理学院 黑龙江哈尔滨 150081
2. School of Health Management, Harbin Medical University, Harbin Heilongjiang 150081, China
当前,对于卫生统计指标和卫生政策效果的分析,以基于微观调查、访谈资料和公报、年鉴等数据的实证研究为主。比如,王怡欢等基于中国健康与养老追踪调查数据(China Health and Retirement Longitudinal Study, CHARLS)分析发现,2018年我国农村贫困家庭灾难性卫生支出发生率和因病致贫率分别为28.20%和32.40%[1];李丹等根据我国卫生健康相关统计公报和年鉴,对2007—2018年我国医疗卫生资源配置的基尼系数及其空间分量进行了梳理分析[2];王贞等利用2013—2017年的城乡居民医保报销数据,研究了医保门诊报销封顶线的设置对居民住院率的影响[3]。而在宏观经济政策和金融政策的研究中,反事实分析方法得到了广泛地应用[4],可以针对不同政策选择,对其实施效果进行充分事前预估,以选择最优改革路径和决策方式,减少政策变革的社会成本。以反事实分析为基础的卫生指标统计和政策效果预估,对于卫生体制改革和卫生政策改良同样有着较高的应用价值,但此类研究在卫生健康领域仍缺乏一定的工具基础和范式标准。
为了解决上述问题,任晓明和吴群红基于Newton-Cotes算法构建了能够估算我国医疗可负担性指标的模型。[5]该模型以国家统计局公布的宏观数据为基础,拟合家庭收入分布和医疗支出分布曲线,构造出我国家庭收入和医疗支出的二维联合分布函数,并将整个概率空间划分为90 000个细分区域,用每个细分区域对应一个异质性家庭,从而估算出全社会的灾难性卫生支出发生率和因病致贫率等指标,并进一步进行政策效果的反事实分析。但是,该模型用于拟合曲线的样本数据相当有限,无法达到经典统计学中数据拟合所需的合理样本量,同时,对于分布函数的选择并没有经过详细的论证。本研究在任晓明和吴群红(Ren & Wu,RW)模型基础上对原有的不合理之处进行改进,以北京大学中国家庭追踪调查(China Family Panel Studies,CFPS)数据相关字段为基础拟合两种分布曲线,并充分比较了各分布函数拟合回归的整体效果,筛选出了最优的分布函数,还对模型应用场景进行拓展,从而提升估算结果的准确度和模型的整体应用价值,能实现更具现实依据的参数估算和反事实分析。为了行文方便,本研究后续将从居民家庭收入五等分数据等宏观数据出发,拟合分布曲线,构造虚拟社群,进行卫生指标估算和反事实分析的模型,简称为RW原始模型;将以CFPS数据等微观大样本数据出发,拟合分布曲线,构造虚拟社群,进行卫生指标估算和反事实分析的模型,简称为RW拓展模型。
1 RW拓展模型具体算法 1.1 分布曲线的拟合利用CFPS数据库统计的样本家庭在2012、2014、2016、2018和2020年过去12个月“全部家庭纯收入”字段,将最高收入和最低收入之间划分为不同的收入区间,用各区间内的家庭数量和占比,拟合各年度的家庭收入分布情况。由于家庭收入分布差异较大,高收入家庭在数轴上的分布极为稀疏,样本数据在各个数值区间的分布也并不十分平滑,如果直接拟合概率密度函数(Probability Density Function,PDF),将会带来相当多的系统误差,因此,本研究选择累计密度函数(Cumulative Distribution Function,CDF)作为拟合对象。类似的,利用CFPS数据库中的衡量样本家庭各年度自付费用的“医疗保健支出”字段,拟合各年度的家庭卫生支出分布情况。
收入和医疗支出分布的估算一般可以采用对数正态分布(LogNormal)、对数逻辑分布(LogLogistic)、贝塔分布(Beta)、伽玛分布(Gamma)、威布尔分布(Weibull)以及指数分布(Exponential)等。虽然此前研究表明,各个分布的拟合效果各有优缺点[6],但为了排除拟合效果的样本依赖性,本研究依照各个分布函数分别进行了拟合。以2020年家庭收入数据为例,各拟合方式的特征参数、均方根误差(RMSE)、赤池信息准则(AIC)和贝叶斯信息准则(BIC)值参见表 1。
| 表 1 各分布函数拟合结果 |
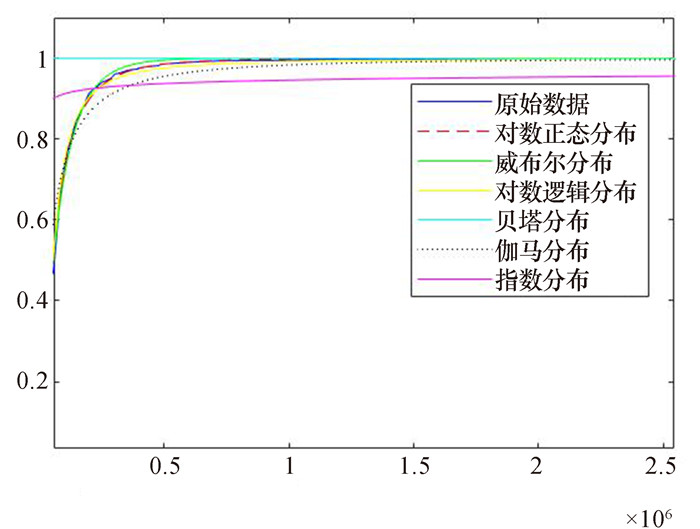
对比表 1中各拟合的RMSE、AIC和BIC值,以及图 1中各拟合的直观效果,可以发现,威布尔分布和对数正态分布的拟合效果好于其他几种分布。各年度的家庭医疗支出曲线的拟合也是如此。这与以往的部分研究结果并不一致[7],表明基于微观数据的拟合效果差异很可能存在样本依赖性。此外,对数正态分布虽然在拟合指标上弱于威布尔分布,但实际拟合图形与原始数据图形十分接近,甚至强于威布尔分布。故而,本研究认为两种分布函数都可以应用于实际拟合过程中。但由于对数正态分布的应用更为广泛,可操作性更强,本研究将以对数正态分布为例进行后续的模型构建和应用。以对数正态分布拟合的各样本年度我国家庭收入和家庭医疗支出的特征指标如表 2所示。
|
图 1 各分布类型拟合CDF曲线对照 |
| 表 2 我国家庭收入和医疗支出估计结果 |
对比RW拓展模型与原始模型的拟合结果[5],可以发现,两者对于各年度家庭收入和医疗支出期望值的拟合结果基本一致,但由于拓展模型样本量更大,有效信息更多,因此拓展模型得到的家庭收入和医疗支出标准差显著大于原始模型。此外,表中2020年家庭医疗支出的突然下降,可能是由于新冠疫情造成的医疗服务量骤减所致。[8]
1.3 构造代表性家庭得到收入和医疗支出分布曲线后,在期望值的左右两侧分别细分为足够多的分区。分区的数量既要考虑到分布的偏性特征,在概率密度较大区域作足够多的分区,也要满足计算经济学中要求的,各分区概率密度之和应当等于1。[9]由于对数正态分布是右偏的长尾分布,因此在期望值左侧平均分为100个分区,右侧做200个分区。虽然左侧分区在绝对数量上较少,但由于右侧的拖尾足够长,因此对期望值左侧的分区实际上是更细致的。此时,整个二维分布的概率空间被细分为90 000个异质性家庭,从而组成了一个虚拟社群,每个异质性家庭有收入、医疗支出、占比三个属性值。异质性家庭的占比为分区上下界的累积概率密度之差。
同时,本研究还发现,CFPS历年数据中家庭收入与医疗保健支出的相关性较弱,回归系数也不显著,因此拓展模型不必假设家庭医疗保健支出会随家庭收入的增长而增长,即两个维度的属性值并不能相互影响。
1.4 估计目标参数鉴于家庭收入和医疗支出的相对独立性,上述拟合的家庭收入曲线和医疗支出曲线,可以单独使用,也可以组合成为二维联合分布函数,或者结合实际问题,增加家庭的异质性维度和属性值,通过分析整合社群中所有异质性家庭的相关属性值,得到需要的参数指标。模型可以估算我国历年的健康筹资公平性参数和医疗可负担性参数,并预估针对某一疾病的特定干预措施的经济性、可负担性和公平性特征,还可以与宏观经济模型相结合[10],估算出不同宏观经济政策以及社会现象可能对社会卫生可负担性和健康筹资公平性带来的综合影响。
2 RW拓展模型的相关应用 2.1 卫生可负担性估计对RW拓展模型构造的异质性家庭进行统计分析,可以得到我国各年度卫生可负担情况,如表 3所示。表中的灾难性卫生支出发生率指一个区域或样本中医疗支出超过家庭支付能力40%的家庭占比。因病致贫率是指由于支付医疗费用落入贫困线以下的原非贫困家庭占所有非贫困家庭之比。灾难性卫生支出的平均差距和相对差距分别由所有家庭卫生支出占比超过40%部分之和除以家庭总数或除以发生灾难性卫生支出家庭数量而得到。集中指数则反映了灾难性卫生支出在不同经济水平的家庭中的分布状况, 小于0表示灾难性卫生支出更多地在低收入水平家庭中发生,大于0表示更多地在高收入水平家庭中发生。用集中指数对发生率和发生强度进行校正就可以得到调整后的发生率和发生强度。表中数据表明,2012年以后,随着我国人均收入的增长,灾难性卫生支出的发生率和因病致贫率基本都处在缓慢下降的趋势当中,平均差距和相对差距等强度指标不断降低,发生率和发生强度的集中程度则都有所增长。这与原始模型估算的指标变化趋势基本一致。[5]
| 表 3 可负担性指标估计结果 |
利用RW拓展模型估算的2012—2020年的健康筹资公平性指标如表 4所示。各指标中,基尼系数衡量的是不同医疗支出家庭分组从低到高排列时,洛伦兹曲线相对于绝对公平线的偏移程度。泰尔指数则是基于信息熵理论,从医疗支出的组内差距和组间差距计算出的不公平程度。变异系数是不同分组医疗支出标准差与平均值的比,用于衡量医疗支出的离散程度。阿特金森指数则衡量的是保持社会总福利不变的等价敏感医疗支出相对于社会平均医疗支出的偏移程度。可见,除2018年之外,各健康筹资公平性指标都在缓慢升高,表明我国医疗筹资的公平性可能处于不断恶化的趋势中。
| 表 4 公平性指标估计结果 |
假定某一特定疾病A不存在家庭聚集性,人群总体患病率为X,传统干预方法F的平均治疗费用为Y1元/年,新干预方法E比传统干预方法F能为每位患者降低平均治疗费用Y2元/年。为了验证广泛推广干预措施E取代干预措施F成为治疗疾病A的主要措施后社会可负担性的变化,可以采用上述RW拓展模型,将虚拟的异质性家庭继续划分为疾病A的患病家庭和非患病家庭。根据两个不相关的随机变量的运算公式,比较出推广干预措施E后的灾难性卫生支出发生率和因病返贫率变化值,及受影响的家庭数。下面假定X=10%,Y1=5 000,Y2=1 000,以2020年作为基准年,估算干预措施E覆盖疾病A患者的20%、50%和100%的结果(表 5)。可见,随着干预措施E的推广,社会可负担性持续好转,发生灾难性卫生支出和因病返贫的家庭数量不断减少。
| 表 5 推广干预措施E的社会可负担性估计 |
在当前药品带量采购政策进行中,如何评估带量采购政策效果意义重大。利用上述RW拓展模型,以2020年为基准年,根据带量采购药物在全部药物中的市场占比将带量采购药物价格降幅转化为全药价格水平降幅,进而估计出不同全药价格水平变化对社会可负担性参数的影响,具体估计结果见表 6。可见,随着带量采购导致药品价格不断降低,灾难性卫生支出发生率、因病致贫率和发生强度等指标不断降低,卫生可负担性显著改善。
| 表 6 推进药品带量采购的长期效应数值模拟(2012) |
一般来说,经典计量回归中数据拟合所需的样本量最少为30个,样本量过少则无法满足残差服从正态分布的基本假设[11],从而产生理论基础上的漏洞。RW原始模型以国家统计局公布的居民家庭按收入五等分分组数据拟合家庭收入分布曲线,以三种典型疾病的医疗费用和住院率拟合医疗支出分布曲线,每次拟合所用样本量仅为3个或5个,难以满足拟合回归对样本量的基本要求,无法提供足够的居民收入和医疗支出离散程度信息,从而使得对两者方差的估计值显著偏小。[5]而RW拓展模型则以CFPS数据相关字段为基础拟合两种分布曲线,每次拟合所用样本量在11 000个家庭以上,远大于30个样本量的基本要求,对收入和医疗支出方差值的估计也分别从0.8和0.75提升到1.05和1.8左右,弥补了方差值过小的问题,使得收入分布图形右偏的特征得到更充分的体现[12],模型的推导过程和估算结果更具现实依据。因此,虽然RW原始模型与RW拓展模型对收入和医疗支出期望值的估计结果以及各主要指标的变化趋势基本一致,但是RW拓展模型采用大样本微观数据作为模型基础,对数据离散程度的估计更为精准,提升了拟合的准确性。
3.2 RW拓展模型的分布函数选择更为严谨,逻辑链条更为严密RW原始模型借鉴其他研究和应用场景下各分布函数拟合效果的既有结论[6],仅对相关分布进行了单一拟合,而没有考虑数据拟合效果可能存在一定的样本依赖性,不同数据基础下各分布函数的拟合效果可能存在差异。特别是,不同数据来源拟合的样本依赖性和复杂系统的不确定性,已经引起了越来越多的重视[13-14],因此有必要对分布函数的选择过程进行更细致的推导。RW拓展模型对常见的6种分布函数分别进行拟合,全面比较了各拟合方法的RMSE、AIC和BIC等效果参数和拟合图形的一致性,发现除了RW原始模型所采用的对数正态分布以外,威布尔分布相较其他分布函数的拟合效果更好,也可以应用于后续的模型推导和反事实分析中。这一过程补充了RW原始模型推导过程中遗漏的逻辑链条,提升了模型构建和应用的严谨性和可靠性。
3.3 RW拓展模型的应用前景更为广阔,应用价值更高由于RW原始模型基础数据样本量有限,对居民收入和医疗支出离散程度的估计值偏小,产生了两个限制模型大范围应用的问题。其一是对基尼系数、泰尔指数和阿特金森指数等依赖离散程度的公平性指标的估计效果较差。其二是在应对某些参数变化时欠缺稳健性,常常得出异常估计结果。原因在于,在本研究情境下,上述右偏分布函数的期望值越大,方差越小,那么图形的左尾部越薄,低收入人群的占比越小。[12]由于RW原始模型的方差已经很小,在收入期望值产生微小提升时,低收入人群占比迅速减小,灾难性卫生支出发生率等指标就会产生相当大的缩减和改变,甚至得到异常估计结果,无法实现不同情境下的政策效果对比和更广泛的应用。RW拓展模型提升了收入和医疗支出方差的估计值后,弥补了上述两方面不足,对图形厚尾特征的估计更加合理,模型的应用场景获得了提升,不仅可以估算出更为合理的健康筹资公平性参数和医疗可负担性参数,并且能够更为稳健地应用于多种干预效果预估和反事实分析场景中,具备了良好的应用前景。
总之,本研究中的RW拓展模型对主要指标参数的估计结果与原始模型基本一致,但由于数据基础丰富,对收入和医疗支出离散程度的估计更为精准,可以对原始模型起到良好的补充和借鉴作用,能较好地应用于卫生可负担性和公平性等参数指标的测算以及卫生经济学评价评估当中。以真实世界的抽样、调查和统计数据为基础,计算出具有一般性的全局分布特征,并构造出符合该分布特征的虚拟社群,在此基础上与大型结构模型不断融合,能进一步搭建具有进行反事实分析能力的虚拟“社会实验室”。[15]本研究在此方向上进行了一些尝试,未来更深入的突破,一方面需要在一定标准下解决如何更好地拟合现实的问题,另一方面需要解决异质性家庭在维度不断增加时的数据存储和运算速度问题,以及在家庭属性之外,如何增加家庭的运动方式和行为方式的问题。
作者声明本文无实际或潜在的利益冲突。
| [1] |
王怡欢, 张楚. 农村贫困家庭灾难性卫生支出风险及影响因素研究: 基于2018年CHARLS数据[J]. 中国卫生政策研究, 2021, 14(1): 44-49. |
| [2] |
李丹, 巢健茜, 孔晶, 等. 基于基尼系数的我国医疗卫生资源的空间匹配研究[J]. 中国卫生统计, 2022, 39(4): 482-486, 493. |
| [3] |
王贞, 封进, 刘一恒. 门诊待遇非线性定价与住院率: 来自城乡居民基本医保的证据[J]. 经济研究, 2023, 58(12): 132-149. |
| [4] |
朱军. 高级财政学Ⅱ: DSGE的视角及应用前沿: 模型分解与编程[M]. 上海: 上海财经大学出版社, 2019.
|
| [5] |
任晓明, 吴群红. 基于Newton-Cotes算法的我国家庭灾难性卫生支出估算研究[J]. 中国卫生经济, 2022, 41(9): 9-12, 18. |
| [6] |
霍振昂, 王仲阳, 孙韬. 住院医疗费用分布拟合研究[J]. 中国卫生统计, 2017, 34(6): 972-974. |
| [7] |
陈建东, 程树磊, 蒲明. 如何准确地拟合居民的收入分布[J]. 北京工商大学学报(社会科学版), 2017, 32(2): 10-20. |
| [8] |
袁波英, 王锦毓, 林凯. 新冠疫情对三级公立医院运营影响研究[J]. 医院管理论坛, 2021, 38(8): 29-32. |
| [9] |
Miranda M J, Fackler P L. Applied computational economics and finance[M]. Boston: MITPress, 2004.
|
| [10] |
任晓明, 吴群红. 人口老龄化对卫生健康水平的影响研究[J]. 卫生经济研究, 2023, 40(1): 6-8, 13. |
| [11] |
魏昙荣, 曾振柄. 正态分布无偏估计相关的一个极限定理[J]. 大学数学, 2022, 38(4): 96-99. |
| [12] |
周雪娇, 李群, 张宝学. 基于混合正态模型的居民收入分布的演化研究[J]. 统计与决策, 2020, 36(3): 21-26. |
| [13] |
傅华栋, 吕京, 宋桂兰. 科研数据不确定性表征方法和评估技术的研究[J]. 质量与认证, 2020(2): 60-62. |
| [14] |
范晓光, 刘金龙. 计算社会学的基础问题及未来挑战[J]. 西安交通大学学报(社会科学版), 2022, 42(1): 38-45. |
| [15] |
吕鹏. ABM仿真模拟方法漫谈[J]. 贵州师范大学学报(社会科学版), 2016, 57(6): 43-45. |
(编辑 薛云)





